《2025年启东中学作业本八年级数学上册苏科版连淮专版》

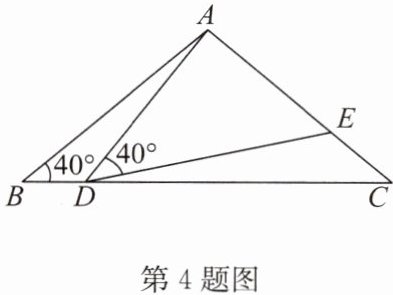
4. (2024·灌云县期末)如图,在 ABC 中,$AB = AC = 2$,$∠B = 40^{\circ}$,点 D 在线段 BC 上运动(点 D 不与点 B,C 重合),连接 AD,作$∠ADE = 40^{\circ}$,DE 交线段 AC 于点 E。
(1) 当$∠BDA = 115^{\circ}$时,$∠EDC = $25$^{\circ}$,$∠AED = $65$^{\circ}$；
(2) 线段 DC 的长度为何值时,$\triangle ABD≌\triangle DCE$,请说明理由。

(2) 解：当$DC=2$时，$\triangle ABD≌ \triangle DCE$，理由如下：
$\because \angle C=40^{\circ }$，$\therefore \angle DEC+\angle EDC=140^{\circ }$．
又$\because \angle ADE=40^{\circ }$，$\therefore \angle ADB+\angle EDC=140^{\circ }$，
$\therefore \angle ADB=\angle DEC$．
又$\because AB=DC=2$，在$\triangle ABD$和$\triangle DCE$中，
$\left\{\begin{array}{l} \angle ADB=\angle DEC,\\ \angle B=\angle C,\\ AB=DC,\end{array}\right.$$\therefore \triangle ABD≌ \triangle DCE(\text{AAS})$．

答案：
(1) $25$ $65$
(2) 解：当$DC=2$时，$\triangle ABD≌ \triangle DCE$，理由如下：
$\because \angle C=40^{\circ }$，$\therefore \angle DEC+\angle EDC=140^{\circ }$．
又$\because \angle ADE=40^{\circ }$，$\therefore \angle ADB+\angle EDC=140^{\circ }$，
$\therefore \angle ADB=\angle DEC$．
又$\because AB=DC=2$，在$\triangle ABD$和$\triangle DCE$中，
$\left\{\begin{array}{l} \angle ADB=\angle DEC,\\ \angle B=\angle C,\\ AB=DC,\end{array}\right.$$\therefore \triangle ABD≌ \triangle DCE(\text{AAS})$．

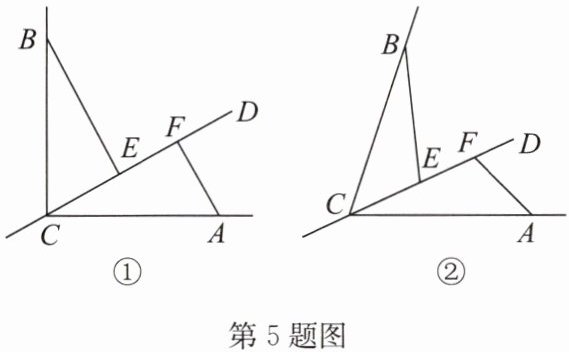
5. 已知 CD 是经过$∠BCA$的顶点 C 的一条直线,$CA = CB$,E,F 分别是直线 CD 上的两点,且$∠BEC = ∠CFA = \alpha$。
(1) 如图①,若$∠BCA = 90^{\circ}$,$\alpha = 90^{\circ}$,则 BE=CF,EF=$|BE - AF|$；(均填“＞”“＜”或“=”)
(2) 如图②,若$0^{\circ} ＜ ∠BCA ＜ 180^{\circ}$,请添加一个关于α与$∠BCA$关系的条件：$\alpha +\angle BCA=180^{\circ }$,使(1)中的两个结论仍然成立,并证明这两个结论。

答案：
(1) $=$ $=$
(2) 解：$\alpha +\angle BCA=180^{\circ }$ 证明如下：
在$\triangle BCE$中，$\angle CBE+\angle BCE=180^{\circ }-\angle BEC=180^{\circ }-\alpha $．
$\because \angle BCA=180^{\circ }-\alpha $，$\therefore \angle CBE+\angle BCE=\angle BCA$．
$\because \angle ACF+\angle BCE=\angle BCA$，$\therefore \angle CBE=\angle ACF$．
$\because \angle BEC=\angle CFA$，$BC=CA$，$\therefore \triangle BCE≌ \triangle CAF(\text{AAS})$，
$\therefore BE=CF$，$CE=AF$．
$\because EF=|CF-CE|$，$\therefore EF=|BE-AF|$．