《2025年启东中学作业本八年级数学上册苏科版连淮专版》

10. (2024·昆山期末)在平面直角坐标系中,把点$P(3,a-1)$向下平移5个单位长度得到点$Q(3,2-2b)$,则代数式$\frac {1}{4}a+\frac {1}{2}b+3$的值为5.

答案： 5

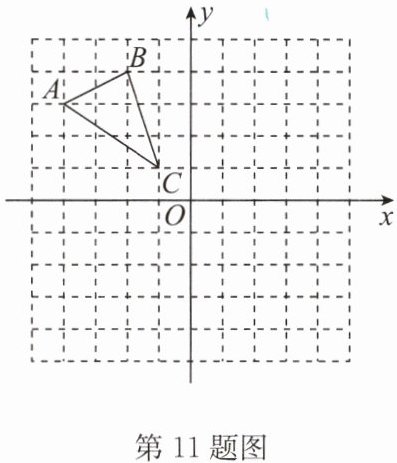
11. (2024·灌云县期末)如图,在平面直角坐标系中,$△ABC三个顶点的坐标分别为A(-4,3),B(-2,4),C(-1,1)$.若$△ABC$向右平移5个单位长度,再向下平移3个单位长度得到$△A'B'C'$,点A,B,C的对应点分别为$A',B',C'$.
(1)写出点$A',B',C'$的坐标:$A'$(1,0),$B'$(3,1),$C'$(4,−2);
(2)在图中画出平移后的$△A'B'C'$;
(3)求出$△ABC$的面积.

(2)解:如答图所示，△A'B'C'即为所作.
(3)解:S△ABC=3×3−$\frac{1}{2}$×3×2−$\frac{1}{2}$×3×1−$\frac{1}{2}$×1×2=9−3−$\frac{3}{2}$−1=$\frac{7}{2}$.

答案：
(1)(1,0)　(3,1)　(4,−2)
(2)解:如答图所示，△A'B'C'即为所作.
(3)解:S△ABC=3×3−$\frac{1}{2}$×3×2−$\frac{1}{2}$×3×1−$\frac{1}{2}$×1×2=9−3−$\frac{3}{2}$−1=$\frac{7}{2}$.

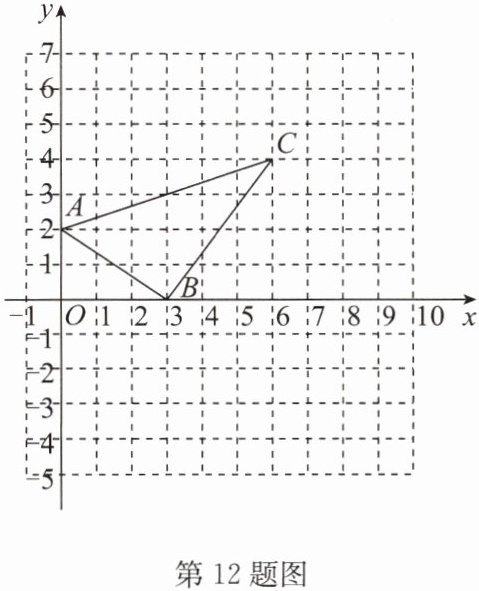
12. (2024·吴江区期末)如图,在平面直角坐标系中,$A(0,2),B(3,0),C(6,4)$.
(1)将$△ABC$向右平移3个单位长度,再向下平移4个单位长度,得到$△A_{1}B_{1}C_{1}$,在方格纸中画出$△A_{1}B_{1}C_{1}$.$△ABC内有一点P(a,b)$,则平移后它的对应点$P_{1}$的坐标是$(a+3,b-4)$.
(2)$△ABC$的面积为9.
(3)在y轴上是否存在点M,使$△AMC的面积等于△ABC$的面积的2倍? 若存在,求出点M的坐标;若不存在,请说明理由.
解:存在.设M(0,m),则AM=|m−2|.
∵△AMC的面积等于△ABC的面积的2倍,
∴$\frac{1}{2}$×6×|m−2|=2×9,
解得m=8或m=−4,
∴点M的坐标为(0,8)或(0,−4).

答案：
(1)解:△A₁B₁C₁如答图所示.　P₁(a+3,b−4)
(2)9
(3)解:存在.设M(0,m),则AM=|m−2|.
∵△AMC的面积等于△ABC的面积的2倍,
∴$\frac{1}{2}$×6×|m−2|=2×9,
解得m=8或m=−4,
∴点M的坐标为(0,8)或(0,−4).