《2025年启东中学作业本八年级数学上册苏科版连淮专版》

8. (2024·惠山区期中)如图,直线 l 上有三个边长分别为 a,b,c 的正方形,则有$a^{2}+c^{2}$=$b^{2}$.(填“＞”“＜”或“=”)

答案： =

9. (2024·灌南县期中)中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用 4 个全等的直角三角形拼成如图所示的“弦图”.在$Rt△ABC$中,$∠ACB= 90^{\circ }$,若$AC= b,BC= a$,请你利用这个图形解决下列问题:
(1)试说明:$a^{2}+b^{2}= c^{2};$
(2)如果大正方形的面积是 12,小正方形的面积是 4,求$(a+b)^{2}$的值.

答案： 解:
(1)
∵大正方形的面积为c²，直角三角形的面积为$\frac{1}{2}$ab,小正方形的面积为(b−a)²,
∴c²=4×$\frac{1}{2}$ab+(b−a)²=2ab+b²−2ab+a²,即c²=a²+b².
(2)根据题意,得(b−a)²=4,4×$\frac{1}{2}$ab=12−4=8,
∴ab=4,
∴(a+b)²=(b−a)²+4ab=4+4×4=20.

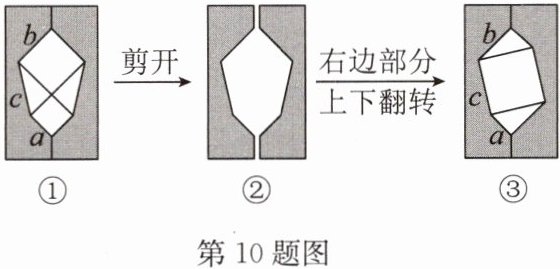
10. (2024·海州区期中)意大利著名画家达·芬奇用如图所示的方法证明了勾股定理,其中图①的空白部分是由两个正方形和两个直角三角形组成,图③的空白部分由两个直角三角形和一个正方形组成.设图①中空白部分的面积为$S_{1}$,图③中空白部分的面积为$S_{2}$.
(1)请用含 a,b,c 的代数式分别表示$S_{1},S_{2};$
(2)请利用达·芬奇的方法证明勾股定理.

答案： 解:
(1)S₁=a²+b²+2×$\frac{1}{2}$ab=a²+b²+ab,S₂=c²+2×$\frac{1}{2}$ab=c²+ab.
(2)由S₁=S₂,得a²+b²+ab=c²+ab,
∴a²+b²=c².

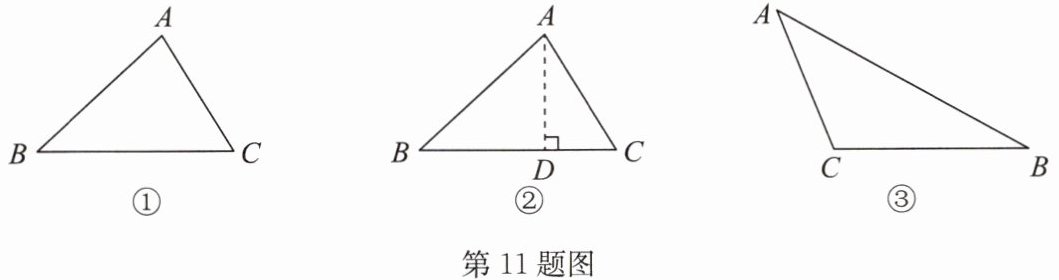
11. (2024·东海县期中)在$△ABC$中,$BC= a,CA= b,AB= c$.若$∠C$为直角,则$a^{2}+b^{2}= c^{2}$;若$∠C$为锐角或钝角,则$a^{2}+b^{2}与c^{2}$之间有怎样的大小关系呢？我们一起进行探究吧.
(1)阅读并填空:如图①,若$∠C$为锐角,求证:$a^{2}+b^{2}＞c^{2}$.
证明:如图②,过点 A 作$AD⊥BC$于点 D,则$BD= BC-CD= a-CD$.
在$Rt△ABD$中,$AD^{2}= AB^{2}-BD^{2},$
在$Rt△ACD$中,$AD^{2}= $____,
∴____,即$c^{2}-(a-CD)^{2}= b^{2}-CD^{2},$
$\therefore a^{2}+b^{2}-c^{2}= 2a\cdot CD.\because a＞0,CD＞0,\therefore a^{2}+b^{2}-c^{2}＞0,\therefore a^{2}+b^{2}＞c^{2}.$
(2)解答问题:如图③,若$∠C$为钝角,试推导$a^{2}+b^{2}与c^{2}$的大小关系.

答案：

(1)AC²−CD²　AB²−BD²=AC²−CD²
(2)解:如答图，过点A作AD⊥BC交BC的延长线于点D,

则BD=BC+CD=a+CD.
在Rt△ABD中,AD²=AB²−BD²,
在Rt△ACD中,AD²=AC²−CD²,
∴AB²−BD²=AC²−CD²,
即c²−(a+CD)²=b²−CD²,
∴a²+b²−c²=−2a·CD.
∵a＞0,CD＞0,
∴a²+b²−c²＜0,
∴a²+b²＜c².