《2025年启东中学作业本八年级数学上册苏科版连淮专版》

9. 已知$a$,$b$,$c为\triangle ABC$的三边,且满足$a^{2}c^{2}-b^{2}c^{2}= a^{4}-b^{4}$,则$\triangle ABC$为等腰或直角三角形.

答案： 等腰或直角

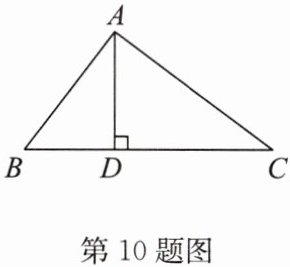
10. (2024·宿豫区期中)如图,在$\triangle ABC$中,$AD\perp BC$,垂足为$D$,且$AB = 15$,$AD = 12$,$CD = 16$.求证:$\triangle ABC$是直角三角形.

答案： 解：
在$Rt\triangle ABD$中，根据勾股定理$BD=\sqrt{AB^{2}-AD^{2}}$，已知$AB = 15$，$AD = 12$，则$BD=\sqrt{15^{2}-12^{2}}=\sqrt{225 - 144}=\sqrt{81}=9$。
又因为$CD = 16$，所以$BC=BD + CD=9 + 16=25$。
在$Rt\triangle ADC$中，根据勾股定理$AC=\sqrt{AD^{2}+CD^{2}}$，$AD = 12$，$CD = 16$，则$AC=\sqrt{12^{2}+16^{2}}=\sqrt{144 + 256}=\sqrt{400}=20$。
在$\triangle ABC$中，$AB = 15$，$AC = 20$，$BC = 25$。
因为$AB^{2}+AC^{2}=15^{2}+20^{2}=225 + 400 = 625$，$BC^{2}=25^{2}=625$，即$AB^{2}+AC^{2}=BC^{2}$。
根据勾股定理的逆定理，所以$\triangle ABC$是直角三角形。

11. (2024·灌南县期中)【知识背景】我国古代把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”. 据《周髀算经》记载,公元前 1000 多年就发现了“勾三股四弦五”的结论. 像 3,4,5 这样能作为直角三角形三边长的 3 个正整数,称为勾股数.
请你观察下列三组勾股数：(3,4,5);(5,12,13);(7,24,25);…;分析其中的规律,可以发现这些勾股数的勾都是奇数,且从 3 起就没有间断过. 当勾为 3 时,股$4= \frac{1}{2}×(9 - 1)$,弦$5= \frac{1}{2}×(9 + 1)$;当勾为 5 时,股$12= \frac{1}{2}×(25 - 1)$,弦$13= \frac{1}{2}×(25 + 1)$;当勾为 7 时,股$24= \frac{1}{2}×(49 - 1)$,弦$25= \frac{1}{2}×(49 + 1)$.
(1)若勾用$n(n\geqslant3$,且$n$为奇数)表示,请用含有$n$的式子表示股和弦,则股= ______$\frac{1}{2}(n^{2}-1)$,弦= ______$\frac{1}{2}(n^{2}+1)$,据此规律写出第四组勾股数是______$(9,40,41)$;
(2)若$a = m^{2}-1$,$b = 2m$,$c = m^{2}+1$,其中$m＞1且m$是整数. 求证:以$a$,$b$,$c为边的\triangle ABC$是直角三角形.
证明：$\because a=m^{2}-1,b=2m,c=m^{2}+1$,其中$m＞1$且$m$是整数,
$(m^{2}-1)^{2}+(2m)^{2}=m^{4}-2m^{2}+1+4m^{2}=m^{4}+2m^{2}+1=(m^{2}+1)^{2}$,
$\therefore a^{2}+b^{2}=c^{2},\therefore$以$a,b,c$为边的$\triangle ABC$是直角三角形.

答案：
(1) $\frac{1}{2}(n^{2}-1)$ $\frac{1}{2}(n^{2}+1)$ $(9,40,41)$;
(2) 证明：$\because a=m^{2}-1,b=2m,c=m^{2}+1$,其中$m＞1$且$m$是整数,
$(m^{2}-1)^{2}+(2m)^{2}=m^{4}-2m^{2}+1+4m^{2}=m^{4}+2m^{2}+1=(m^{2}+1)^{2}$,
$\therefore a^{2}+b^{2}=c^{2},\therefore$以$a,b,c$为边的$\triangle ABC$是直角三角形.