第92页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. [2024·宜宾中考]如图,AB 是$\odot O$的直径,若$∠CDB= 60^{\circ }$,则$∠ABC$的度数等于(
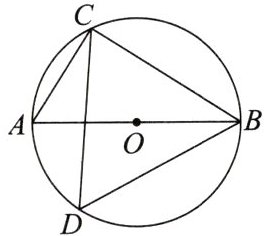
A. $30^{\circ }$
B. $45^{\circ }$
C. $60^{\circ }$
D. $90^{\circ }$
A
)
A. $30^{\circ }$
B. $45^{\circ }$
C. $60^{\circ }$
D. $90^{\circ }$
答案:
A
2. [2024·甘肃中考]如图,点 A,B,C 在$\odot O$上,$AC⊥OB$,垂足为点 D. 若$∠A= 35^{\circ }$,则$∠C$的度数是(
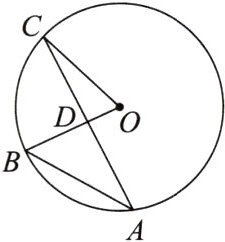
A. $20^{\circ }$
B. $25^{\circ }$
C. $30^{\circ }$
D. $35^{\circ }$
A
)
A. $20^{\circ }$
B. $25^{\circ }$
C. $30^{\circ }$
D. $35^{\circ }$
答案:
A
3. 如图,五边形 ABCDE 内接于$\odot O$,$BC= DE$,连接 AC,AD,求证:$∠BCD+∠CAE= 180^{\circ }$.
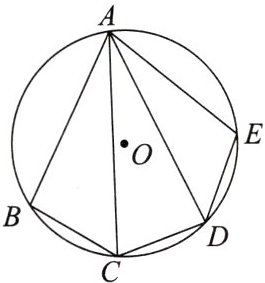
证明:因为$BC = DE$,所以$\overset{\frown}{BC}=\overset{\frown}{DE}$,则$\overset{\frown}{BCD}=\overset{\frown}{CDE}$。
由圆周角定理可知$\angle CAE$所对弧为$\overset{\frown}{CDE}$,$\angle BCD$所对弧为$\overset{\frown}{BAD}$,且$\overset{\frown}{BCD}+\overset{\frown}{BAD}=360^{\circ}$。
根据圆周角与弧的关系,可得$\angle BCD+\angle CAE = 180^{\circ}$。

证明:因为$BC = DE$,所以$\overset{\frown}{BC}=\overset{\frown}{DE}$,则$\overset{\frown}{BCD}=\overset{\frown}{CDE}$。
由圆周角定理可知$\angle CAE$所对弧为$\overset{\frown}{CDE}$,$\angle BCD$所对弧为$\overset{\frown}{BAD}$,且$\overset{\frown}{BCD}+\overset{\frown}{BAD}=360^{\circ}$。
根据圆周角与弧的关系,可得$\angle BCD+\angle CAE = 180^{\circ}$。
答案:
【解析】:
因为$BC = DE$,根据在同圆或等圆中,相等的弦所对的弧相等,所以$\overset{\frown}{BC}=\overset{\frown}{DE}$。
那么$\overset{\frown}{BC}+\overset{\frown}{CD}=\overset{\frown}{DE}+\overset{\frown}{CD}$,即$\overset{\frown}{BCD}=\overset{\frown}{CDE}$。
根据圆周角定理:同弧或等弧所对的圆周角相等,所以$\angle CAE=\angle CAD + \angle DAE$,又因为$\angle CAD$所对的弧是$\overset{\frown}{CD}$,$\angle DAE$所对的弧是$\overset{\frown}{DE}$,所以$\angle CAE$所对的弧是$\overset{\frown}{CDE}$。
而$\angle BCD$所对的弧是$\overset{\frown}{BAD}$,五边形$ABCDE$内接于$\odot O$,整个圆周角为$360^{\circ}$,$\overset{\frown}{BCD}$与$\overset{\frown}{BAD}$组成整个圆周,$\angle BCD$是$\overset{\frown}{BAD}$所对的圆周角,$\angle CAE$是$\overset{\frown}{CDE}$($\overset{\frown}{BCD}$)所对的圆周角。
根据圆内接四边形对角互补的性质(可推广到圆内接多边形中角与弧的关系),$\angle BCD$与$\angle CAE$所对的弧之和为整个圆周,所以$\angle BCD+\angle CAE = 180^{\circ}$。
【答案】:
因为$BC = DE$,所以$\overset{\frown}{BC}=\overset{\frown}{DE}$,则$\overset{\frown}{BCD}=\overset{\frown}{CDE}$。
由圆周角定理可知$\angle CAE$所对弧为$\overset{\frown}{CDE}$,$\angle BCD$所对弧为$\overset{\frown}{BAD}$,且$\overset{\frown}{BCD}+\overset{\frown}{BAD}=360^{\circ}$。
根据圆周角与弧的关系,可得$\angle BCD+\angle CAE = 180^{\circ}$。
因为$BC = DE$,根据在同圆或等圆中,相等的弦所对的弧相等,所以$\overset{\frown}{BC}=\overset{\frown}{DE}$。
那么$\overset{\frown}{BC}+\overset{\frown}{CD}=\overset{\frown}{DE}+\overset{\frown}{CD}$,即$\overset{\frown}{BCD}=\overset{\frown}{CDE}$。
根据圆周角定理:同弧或等弧所对的圆周角相等,所以$\angle CAE=\angle CAD + \angle DAE$,又因为$\angle CAD$所对的弧是$\overset{\frown}{CD}$,$\angle DAE$所对的弧是$\overset{\frown}{DE}$,所以$\angle CAE$所对的弧是$\overset{\frown}{CDE}$。
而$\angle BCD$所对的弧是$\overset{\frown}{BAD}$,五边形$ABCDE$内接于$\odot O$,整个圆周角为$360^{\circ}$,$\overset{\frown}{BCD}$与$\overset{\frown}{BAD}$组成整个圆周,$\angle BCD$是$\overset{\frown}{BAD}$所对的圆周角,$\angle CAE$是$\overset{\frown}{CDE}$($\overset{\frown}{BCD}$)所对的圆周角。
根据圆内接四边形对角互补的性质(可推广到圆内接多边形中角与弧的关系),$\angle BCD$与$\angle CAE$所对的弧之和为整个圆周,所以$\angle BCD+\angle CAE = 180^{\circ}$。
【答案】:
因为$BC = DE$,所以$\overset{\frown}{BC}=\overset{\frown}{DE}$,则$\overset{\frown}{BCD}=\overset{\frown}{CDE}$。
由圆周角定理可知$\angle CAE$所对弧为$\overset{\frown}{CDE}$,$\angle BCD$所对弧为$\overset{\frown}{BAD}$,且$\overset{\frown}{BCD}+\overset{\frown}{BAD}=360^{\circ}$。
根据圆周角与弧的关系,可得$\angle BCD+\angle CAE = 180^{\circ}$。
4. 如图,圆内接四边形 ABCD 的两组对边的延长线分别相交于点 E,F. 若$∠E= 30^{\circ }$,$∠F= 40^{\circ }$,则$∠A= $(
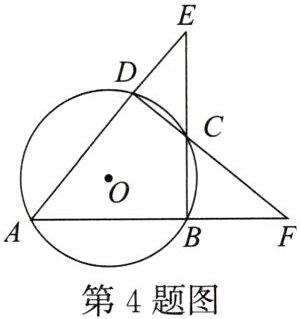
A. $25^{\circ }$
B. $30^{\circ }$
C. $40^{\circ }$
D. $55^{\circ }$
D
)
A. $25^{\circ }$
B. $30^{\circ }$
C. $40^{\circ }$
D. $55^{\circ }$
答案:
D
5. [2023·襄阳中考]如图,四边形 ABCD 内接于$\odot O$,点 E 在 CD 的延长线上. 若$∠ADE= 70^{\circ }$,则$∠AOC= $______
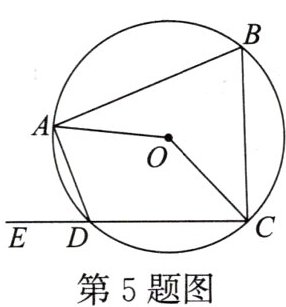
140
$^{\circ }$.
答案:
140
6. [一题多解题]如图,AB 是$\odot O$的直径,AC 是弦,D 是$\overset{\frown }{AC}$上一点,P 是 AB 延长线上一点,连接 AD,DC,CP. 求证:$∠ADC-∠BAC= 90^{\circ }$.(请用两种方法解答)
证明:证法 1:连接 BD.
∵AB 是⊙O 的直径,∴∠ADB =
∵∠ADC - ∠BDC = ∠ADB,∠BDC =
∴∠ADC - ∠BAC = 90°.
证法 2:连接 BC.
∵AB 是⊙O 的直径,∴∠ACB =
∵∠PBC = ∠BAC + ∠ACB,
∴∠PBC - ∠BAC =
∵四边形 ABCD 为⊙O 的内接四边形,
∴∠ADC + ∠ABC =
∵∠PBC + ∠ABC =
∴∠ADC =
∴∠ADC - ∠BAC = 90°.
证明:证法 1:连接 BD.
∵AB 是⊙O 的直径,∴∠ADB =
90°
.∵∠ADC - ∠BDC = ∠ADB,∠BDC =
∠BAC
,∴∠ADC - ∠BAC = 90°.
证法 2:连接 BC.
∵AB 是⊙O 的直径,∴∠ACB =
90°
.∵∠PBC = ∠BAC + ∠ACB,
∴∠PBC - ∠BAC =
90°
.∵四边形 ABCD 为⊙O 的内接四边形,
∴∠ADC + ∠ABC =
180°
.∵∠PBC + ∠ABC =
180°
,∴∠ADC =
∠PBC
,∴∠ADC - ∠BAC = 90°.
答案:
证明:证法 1:连接 BD.
∵AB 是⊙O 的直径,
∴∠ADB = 90°.
∵∠ADC - ∠BDC = ∠ADB,∠BDC = ∠BAC,
∴∠ADC - ∠BAC = 90°.
证法 2:连接 BC.
∵AB 是⊙O 的直径,
∴∠ACB = 90°.
∵∠PBC = ∠BAC + ∠ACB,
∴∠PBC - ∠BAC = 90°.
∵四边形 $ABCD$ 为$\odot O$ 的内接四边形,
∴$\angle ADC+\angle ABC = 180^{\circ}$。
∵$\angle PBC+\angle ABC = 180^{\circ}$,
∴$\angle ADC=\angle PBC$,
∵$\angle ADC=\angle BAC = 90^{\circ}$
∵AB 是⊙O 的直径,
∴∠ADB = 90°.
∵∠ADC - ∠BDC = ∠ADB,∠BDC = ∠BAC,
∴∠ADC - ∠BAC = 90°.
证法 2:连接 BC.
∵AB 是⊙O 的直径,
∴∠ACB = 90°.
∵∠PBC = ∠BAC + ∠ACB,
∴∠PBC - ∠BAC = 90°.
∵四边形 $ABCD$ 为$\odot O$ 的内接四边形,
∴$\angle ADC+\angle ABC = 180^{\circ}$。
∵$\angle PBC+\angle ABC = 180^{\circ}$,
∴$\angle ADC=\angle PBC$,
∵$\angle ADC=\angle BAC = 90^{\circ}$
查看更多完整答案,请扫码查看


