《2025年课时A计划九年级数学上册人教版》

11. 某农场去年种植了$10$亩地的南瓜,亩产量为$2000kg$,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜.已知南瓜种植面积的增长率是亩产量增长率的$2$倍,今年南瓜的总产量为$60000kg$,求南瓜亩产量的增长率.

答案： 解：设南瓜亩产量的增长率为$x$，则南瓜种植面积的增长率为$2x$。
依题意，得$2000(1+x)\times 10(1+2x)=60000$，
整理，得$2x^{2}+3x-2=0$，
解得$x_{1}=\frac{1}{2}=50\%$，$x_{2}=-2$（不符合题意，舍去）。
答：南瓜亩产量的增长率为$50\%$。

12. 如图所示,甲、乙两人分别从正方形花坛$ABCD$的顶点$B,C$同时出发,甲由点$B$向点$C$运动,乙由点$C$向点$D$运动,甲的速度为$2$米/分钟,乙的速度为$1$米/分钟.若正方形花坛的周长为$40$米,问几分钟后,两人相距$2\sqrt {10}$米?

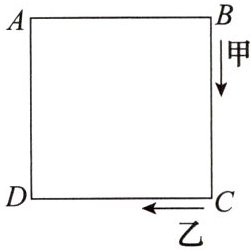
解：设$x$分钟后，两人相距$2\sqrt{10}$米，此时甲运动到点$E$，乙运动到点$F$，则$FC=x$米，$EC=(10-2x)$米。
在$Rt\triangle EFC$中，得$x^{2}+(10-2x)^{2}=(2\sqrt{10})^{2}$，
解得$x_{1}=$2，$x_{2}=6$（不符合题意，舍去）。
答：2分钟后，两人相距$2\sqrt{10}$米。

答案： 解：设$x$分钟后，两人相距$2\sqrt{10}$米，此时甲运动到点$E$，乙运动到点$F$，则$FC=x$米，$EC=(10-2x)$米。
在$Rt\triangle EFC$中，得$x^{2}+(10-2x)^{2}=(2\sqrt{10})^{2}$，
解得$x_{1}=2$，$x_{2}=6$（不符合题意，舍去）。
答：$2$分钟后，两人相距$2\sqrt{10}$米。

13. 某艺术街区进行绿化改造,用一段长$40m的篱笆和一面长15m的墙AB$,围成一个长方形的花园,设平行于墙的一边$DE的长为x m$.
(1)如图$1$,如果长方形花园的一边靠墙$AB$,另三边由篱笆$CDEF$围成,当花园面积为$150m^{2}$时,求$x$的值;$x$的值为10
(2)如图$2$,如果长方形花园的一边由墙$AB和一节篱笆BF$构成,另三边由篱笆$ADEF$围成,当花园面积是$150m^{2}$时,求$BF$的长.$BF$的长为5m.

答案： 解：
(1)由题意，得$\frac{1}{2}(40-x)x=150(0＜x\leq 15)$，
解得$x_{1}=10$，$x_{2}=30$（舍去），
所以$x$的值为$10$。
(2)设$BF$的长为$y$m。
由题意，得$\frac{1}{2}(25-2y)(y+15)=150$，
解得$y_{1}=-\frac{15}{2}$（舍去），$y_{2}=5$。
答：$BF$的长为$5$m。

14. [2024·淮南期末]某水果基地种植了大量的脐橙,$10$月份是脐橙成熟的高峰期,该月脐橙产量达到了$50t$,此后每个月脐橙的产量逐渐减少,到$12$月份时,脐橙的产量为$32t$.
(1)求该基地$11$,$12$两个月脐橙产量的平均减少率是多少?
(2)$10$月份,一水果批发商从该基地以$4元/kg的价格购进了脐橙2000kg$,此时脐橙的市场零售价是$5元/kg$.如果将这批脐橙放在冷库中冷藏起来,每个星期需要支付$400$元的冷藏费用,且每个星期脐橙会自然损坏$40kg$,但是每个星期脐橙的市场零售价会上涨$1元/kg$.若将这批脐橙从冷库中提取出来后能一次性卖完,为了尽快清空库存,求这批脐橙冷藏几个星期后出售可以获得利润$6320$元?

答案： 解：
(1)设该基地$11$，$12$两个月脐橙产量的平均减少率是$x$。
由题意，得$50(1-x)^{2}=32$，
解得$x_{1}=0.2=20\%$，$x_{2}=1.8$（不合题意，舍去）。
答：该基地$11$，$12$两个月脐橙产量的平均减少率是$20\%$。
(2)设这批脐橙冷藏$y$个星期后出售可以获得利润$6320$元，则脐橙会自然损坏$40y$kg。
由题意，得$(5+y-4)(2000-40y)-400y=6320$，
解得$y_{1}=3$，$y_{2}=36$（不合题意，舍去）。
答：这批脐橙冷藏$3$个星期后出售可以获得利润$6320$元。