第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. [2024·凉山州中考]抛物线$ y = \frac { 2 } { 3 } ( x - 1 ) ^ { 2 } + c $经过$ ( - 2, y _ { 1 } ) , ( 0, y _ { 2 } ) , ( \frac { 5 } { 2 }, y _ { 3 } ) $三点,则 y _ { 1 } , y _ { 2 } , y _ { 3 } 的大小关系正确的是(
A. $ y _ { 1 } > y _ { 2 } > y _ { 3 } $
B. $ y _ { 2 } > y _ { 3 } > y _ { 1 } $
C. $ y _ { 3 } > y _ { 1 } > y _ { 2 } $
D. $ y _ { 1 } > y _ { 3 } > y _ { 2 } $
D
)A. $ y _ { 1 } > y _ { 2 } > y _ { 3 } $
B. $ y _ { 2 } > y _ { 3 } > y _ { 1 } $
C. $ y _ { 3 } > y _ { 1 } > y _ { 2 } $
D. $ y _ { 1 } > y _ { 3 } > y _ { 2 } $
答案:
D
2. [2024·齐齐哈尔中考]如图,二次函数$ y = a x ^ { 2 } + b x + 2 ( a \neq 0 ) $的图象与x轴交于$ ( - 1,0 ) $,$ ( x _ { 1 }, 0 ) $,其中$ 2 < x _ { 1 } < 3 $.结合图象给出下列结论:①$ a b > 0 $;②$ a - b = - 2 $;③当$ x > 1 $时,y随x的增大而减小;④关于x的一元二次方程$ a x ^ { 2 } + b x + 2 = 0 ( a \neq 0 ) 的另一个根是 - \frac { 2 } { a } $;⑤b的取值范围为$ 1 < b < \frac { 4 } { 3 } $.其中正确结论的个数是(

A. 2
B. 3
C. 4
D. 5
C
)
A. 2
B. 3
C. 4
D. 5
答案:
C
3. [2024·辽宁中考]如图,在平面直角坐标系中,抛物线$ y = a x ^ { 2 } + b x + 3 $与x轴相交于点A,B,点B的坐标为$ ( 3,0 ) $.若点$ C ( 2,3 ) $在抛物线上,则AB的长为

4
.
答案:
4
4. [2024·陕西中考]一条河上横跨着一座宏伟壮观的悬索桥.桥梁的缆索$ L _ { 1 } 与缆索 L _ { 2 } $均呈抛物线型,桥塔AO与桥塔BC均垂直于桥面,如图所示,以O为原点,以直线$ F F ^ { \prime } $为x轴,以桥塔AO所在直线为y轴,建立平面直角坐标系.
已知缆索$ L _ { 1 } 所在抛物线与缆索 L _ { 2 } $所在抛物线关于y轴对称,桥塔AO与桥塔BC之间的距离$ O C = 100 \mathrm { m } $,$ A O = B C = 17 \mathrm { m } $,缆索$ L _ { 1 } $的最低点P到$ F F ^ { \prime } 的距离 P D = 2 \mathrm { m } $(桥塔的粗细忽略不计).
(1)求缆索$ L _ { 1 } $所在抛物线的函数解析式;
(2)点E在缆索$ L _ { 2 } $上,$ E F \perp F F ^ { \prime } $,且$ E F = 2.6 \mathrm { m } $,$ F O < O D $,求FO的长.
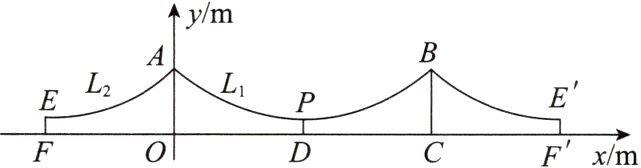
(1)缆索$ L _ { 1 } $所在抛物线的函数解析式为
(2)FO的长为
已知缆索$ L _ { 1 } 所在抛物线与缆索 L _ { 2 } $所在抛物线关于y轴对称,桥塔AO与桥塔BC之间的距离$ O C = 100 \mathrm { m } $,$ A O = B C = 17 \mathrm { m } $,缆索$ L _ { 1 } $的最低点P到$ F F ^ { \prime } 的距离 P D = 2 \mathrm { m } $(桥塔的粗细忽略不计).
(1)求缆索$ L _ { 1 } $所在抛物线的函数解析式;
(2)点E在缆索$ L _ { 2 } $上,$ E F \perp F F ^ { \prime } $,且$ E F = 2.6 \mathrm { m } $,$ F O < O D $,求FO的长.

(1)缆索$ L _ { 1 } $所在抛物线的函数解析式为
$ y = \frac{3}{500}(x - 50)^{2} + 2 $
。(2)FO的长为
40
m。
答案:
解:
(1)缆索 $ L_{1} $ 所在抛物线的函数解析式为 $ y = \frac{3}{500}(x - 50)^{2} + 2 $。
(2) $ FO $ 的长为 40 m。
(1)缆索 $ L_{1} $ 所在抛物线的函数解析式为 $ y = \frac{3}{500}(x - 50)^{2} + 2 $。
(2) $ FO $ 的长为 40 m。
5. [2024·威海中考节选]已知抛物线$ y = x ^ { 2 } + b x + c ( b < 0 ) $与x轴交点的坐标分别为$ ( x _ { 1 }, 0 ) $,$ ( x _ { 2 }, 0 ) $,且$ x _ { 1 } < x _ { 2 } $.
(1)若抛物线$ y _ { 1 } = x ^ { 2 } + b x + c + 1 ( b < 0 ) $与x轴交点的坐标分别为$ ( x _ { 3 }, 0 ) $,$ ( x _ { 4 }, 0 ) $,且$ x _ { 3 } < x _ { 4 } $.
试判断下列每组数据的大小(填写“<”“=”或“>”):
(ⅰ)$ x _ { 1 } + x _ { 2 } $____
(ⅱ)$ x _ { 1 } - x _ { 3 } $____
(ⅲ)$ x _ { 2 } + x _ { 3 } $____
(2)若$ x _ { 1 } = 1 $,$ 2 < x _ { 2 } < 3 $,求b的取值范围.
(1)若抛物线$ y _ { 1 } = x ^ { 2 } + b x + c + 1 ( b < 0 ) $与x轴交点的坐标分别为$ ( x _ { 3 }, 0 ) $,$ ( x _ { 4 }, 0 ) $,且$ x _ { 3 } < x _ { 4 } $.
试判断下列每组数据的大小(填写“<”“=”或“>”):
(ⅰ)$ x _ { 1 } + x _ { 2 } $____
=
$ x _ { 3 } + x _ { 4 } $;(ⅱ)$ x _ { 1 } - x _ { 3 } $____
<
$ x _ { 2 } - x _ { 4 } $;(ⅲ)$ x _ { 2 } + x _ { 3 } $____
>
$ x _ { 1 } + x _ { 4 } $.(2)若$ x _ { 1 } = 1 $,$ 2 < x _ { 2 } < 3 $,求b的取值范围.
-4<b<-3
答案:
解:
(1)(ⅰ) $ = $;(ⅱ) $ < $;(ⅲ) $ > $。
(2) $ \because x_{1} = 1 $,$ 2 < x_{2} < 3 $,
$ \therefore 3 < x_{2} + x_{1} < 4 $,
$ \therefore 3 < -b < 4 $,$ \therefore -4 < b < -3 $。
(1)(ⅰ) $ = $;(ⅱ) $ < $;(ⅲ) $ > $。
(2) $ \because x_{1} = 1 $,$ 2 < x_{2} < 3 $,
$ \therefore 3 < x_{2} + x_{1} < 4 $,
$ \therefore 3 < -b < 4 $,$ \therefore -4 < b < -3 $。
查看更多完整答案,请扫码查看


