第6页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 下列各式是完全平方式的是 (
A. $ a ^ { 2 } + 7 a + 7 $
B. $ m ^ { 2 } - 4 m - 4 $
C. $ x ^ { 2 } - \frac { 1 } { 2 } x + \frac { 1 } { 16 } $
D. $ y ^ { 2 } - 2 y + 2 $
C
)A. $ a ^ { 2 } + 7 a + 7 $
B. $ m ^ { 2 } - 4 m - 4 $
C. $ x ^ { 2 } - \frac { 1 } { 2 } x + \frac { 1 } { 16 } $
D. $ y ^ { 2 } - 2 y + 2 $
答案:
C
2. 若 $ x ^ { 2 } - 2 x - 3 = ( x - 1 ) ^ { 2 } - k $,则 $ k $ 等于 (
A. 1
B. 2
C. 3
D. 4
D
)A. 1
B. 2
C. 3
D. 4
答案:
D
3. [易错题]若 $ x ^ { 2 } - k x + 16 $ 是完全平方式,则 $ k $ 的值是 (
A. -8
B. 8
C. $ \pm 4 $
D. $ \pm 8 $
D
)A. -8
B. 8
C. $ \pm 4 $
D. $ \pm 8 $
答案:
D
4. [教材P9练习第1题改编]在横线上填上适当的数.
(1) $ x ^ { 2 } + 12 x + 36 = ( x + $
(2) $ x ^ { 2 } - 5 x + $
(3) $ x ^ { 2 } + $
(1) $ x ^ { 2 } + 12 x + 36 = ( x + $
6
$ ) ^ { 2 } $;(2) $ x ^ { 2 } - 5 x + $
$\frac{25}{4}$
$ = ( x - $$\frac{5}{2}$
$ ) ^ { 2 } $;(3) $ x ^ { 2 } + $
8
$\cdot x + 9 = ( x + 4 ) ^ { 2 } - $7
.
答案:
(1) 6
(2) $\frac{25}{4}$ $\frac{5}{2}$
(3) 8 7
(1) 6
(2) $\frac{25}{4}$ $\frac{5}{2}$
(3) 8 7
5. [情境题]老师设计了一个接力游戏,用合作的方式完成配方法解方程,规则:每人只能看到前一人给的方程,并进行一步计算,再将结果传递给下一人,最后解出方程,过程如图所示.在接力过程中,自己负责的一步出现错误的是 (
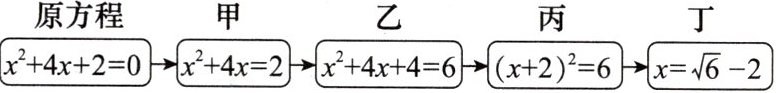
原方程 $ \xrightarrow{\text{甲}} $ $ \xrightarrow{\text{乙}} $ $ \xrightarrow{\text{丙}} $ $ \xrightarrow{\text{丁}} $
A. 只有甲
B. 只有丁
C. 乙和丁
D. 甲和丁
D
)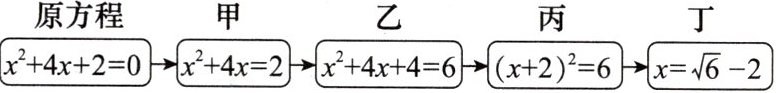
原方程 $ \xrightarrow{\text{甲}} $ $ \xrightarrow{\text{乙}} $ $ \xrightarrow{\text{丙}} $ $ \xrightarrow{\text{丁}} $
A. 只有甲
B. 只有丁
C. 乙和丁
D. 甲和丁
答案:
D
6. 用配方法解方程:
(1) $ x ^ { 2 } + 4 x = 1 $;
(2) $ x ^ { 2 } + 10 x + 16 = 0 $。
(1) $ x ^ { 2 } + 4 x = 1 $;
$x_{1}=-2+\sqrt{5}$,$x_{2}=-2-\sqrt{5}$
(2) $ x ^ { 2 } + 10 x + 16 = 0 $。
$x_{1}=-2$,$x_{2}=-8$
答案:
(1) 解:$x_{1}=-2+\sqrt{5}$,$x_{2}=-2-\sqrt{5}$。
(2) 解:$x_{1}=-2$,$x_{2}=-8$。
(1) 解:$x_{1}=-2+\sqrt{5}$,$x_{2}=-2-\sqrt{5}$。
(2) 解:$x_{1}=-2$,$x_{2}=-8$。
7. 一元二次方程 $ 3 x ^ { 2 } - 12 x + 8 = 0 $ 配方后可化为 (
A. $ ( x - 2 ) ^ { 2 } = \frac { 2 } { 3 } $
B. $ ( 3 x - 2 ) ^ { 2 } = 2 $
C. $ 3 ( x - 2 ) ^ { 2 } = 2 $
D. $ ( x - 2 ) ^ { 2 } = \frac { 4 } { 3 } $
D
)A. $ ( x - 2 ) ^ { 2 } = \frac { 2 } { 3 } $
B. $ ( 3 x - 2 ) ^ { 2 } = 2 $
C. $ 3 ( x - 2 ) ^ { 2 } = 2 $
D. $ ( x - 2 ) ^ { 2 } = \frac { 4 } { 3 } $
答案:
D
8. [与T11互为孪生题]将一元二次方程 $ 2 x ^ { 2 } - 4 x - 1 = 0 $ 化成 $ ( x - 1 ) ^ { 2 } = k $ ( $ k $ 为常数) 的形式,则 $ k $ 的值为 (
A. 1
B. $ \frac { 3 } { 2 } $
C. 2
D. 4
B
)A. 1
B. $ \frac { 3 } { 2 } $
C. 2
D. 4
答案:
B
9. 已知 $ y _ { 1 } = 4 x ^ { 2 } - 4 x + 1 $,$ y _ { 2 } = 4 x - 2 $,则当 $ x = $
$\frac{1}{2}$或$\frac{3}{2}$
时,$ y _ { 1 } = y _ { 2 } $.
答案:
$\frac{1}{2}$或$\frac{3}{2}$
10. 用配方法解方程: $ 2 x ^ { 2 } - 6 x + 1 = 0 $.
解:方程两边同时加上 $ \left( - \frac { 6 } { 2 } \right) ^ { 2 } $, ①
配方,得 $ 2 ( x - 3 ) ^ { 2 } = 8 $, ②
解得 $ x _ { 1 } = 5 $,$ x _ { 2 } = 1 $. ③
请问上述步骤有错误吗? 如果有,请指出,并改正.
解:方程两边同时加上 $ \left( - \frac { 6 } { 2 } \right) ^ { 2 } $, ①
配方,得 $ 2 ( x - 3 ) ^ { 2 } = 8 $, ②
解得 $ x _ { 1 } = 5 $,$ x _ { 2 } = 1 $. ③
请问上述步骤有错误吗? 如果有,请指出,并改正.
解:第①步开始出错,正确步骤如下:
方程两边同时除以2,得$x^{2}-3x+\frac{1}{2}=0$,
配方,得$(x-\frac{3}{2})^{2}=\frac{7}{4}$,
解得$x_{1}=\frac{3+\sqrt{7}}{2}$,$x_{2}=\frac{3-\sqrt{7}}{2}$。
方程两边同时除以2,得$x^{2}-3x+\frac{1}{2}=0$,
配方,得$(x-\frac{3}{2})^{2}=\frac{7}{4}$,
解得$x_{1}=\frac{3+\sqrt{7}}{2}$,$x_{2}=\frac{3-\sqrt{7}}{2}$。
答案:
解:第①步开始出错,正确步骤如下:
方程两边同时除以2,得$x^{2}-3x+\frac{1}{2}=0$,
配方,得$(x-\frac{3}{2})^{2}=\frac{7}{4}$,
解得$x_{1}=\frac{3+\sqrt{7}}{2}$,$x_{2}=\frac{3-\sqrt{7}}{2}$。
方程两边同时除以2,得$x^{2}-3x+\frac{1}{2}=0$,
配方,得$(x-\frac{3}{2})^{2}=\frac{7}{4}$,
解得$x_{1}=\frac{3+\sqrt{7}}{2}$,$x_{2}=\frac{3-\sqrt{7}}{2}$。
查看更多完整答案,请扫码查看


