《2025年课时A计划九年级数学上册人教版》

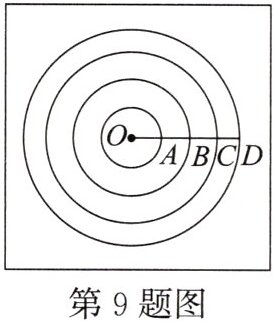
9. [教材P81练习第2题改编]如图是一个由四个同心圆构成的靶子示意图,点O为圆心,且$OA = AB = BC = CD = 5$,那么周长最接近100的圆的半径是(C)

A. OA
B. OB
C. OC
D. OD

答案： C

10. 如图,在$\odot O$中,AB为直径,$CD⊥AB$于点C,四边形CDEF是正方形,连接BD.若$OC = 3,OF = 1$,则BD的长为$4\sqrt{5}$.

答案： $4\sqrt{5}$

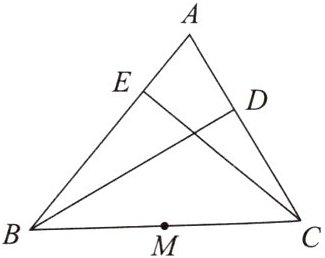
11. [隐圆模型][教材P81练习第3题改编]如图,BD,CE是$\triangle ABC$的高,M为BC的中点.试说明点B,C,D,E在以点M为圆心的同一个圆上.

解：连接ME，MD.
$\because BD$，$CE$ 是 $\triangle ABC$ 的高，$M$ 为 $BC$ 的中点，
$\therefore$ME = MD = MC = MB = \frac{1}{2}BC，
$\therefore$ 由圆的定义可知点 $B$，$C$，$D$，$E$ 在以点 $M$ 为圆心的同一个圆上.

答案： 解：连接 $ME$，$MD$.
$\because BD$，$CE$ 是 $\triangle ABC$ 的高，$M$ 为 $BC$ 的中点，
$\therefore ME = MD = MC = MB = \frac{1}{2}BC$，
$\therefore$ 由圆的定义可知点 $B$，$C$，$D$，$E$ 在以点 $M$ 为圆心的同一个圆上.

12. 如图,AB是$\odot O$的直径,C是$\odot O$上的一点,$CD⊥AB$于点D,$AD ＜ BD$.若$CD = 2cm,AB = 5cm$,求AD1cm,AC$\sqrt{5}$cm的长.

答案： 解：$AD = 1$，$AC = \sqrt{5}$.

13. [探究题][教材P123复习题24第6题改编]
(1)如图,AB是$\odot O$的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设$AB = a$,那么$\odot O的周长L = \pi a$.
探究:①如图1,把AB分成两条相等的线段,每个小圆的周长$L_{2} = \frac{1}{2}\pi a = \frac{1}{2}L$;
②如图2,把AB分成三条相等的线段,每个小圆的周长$L_{3} = $$\frac{1}{3}\pi a$=$\frac{1}{3}L$;
③把AB分成四条相等的线段,每个小圆的周长$L_{4} = $$\frac{1}{4}\pi a$=$\frac{1}{4}L$;
……
④如图3,把AB分成n条相等的线段,每个小圆的周长$L_{n} = $$\frac{1}{n}\pi a$=$\frac{1}{n}L$.
(2)应用:如图,从A地到B地有两条路可走,一条路是大半圆,另一条路是4个小半圆.有一天,一只猫和一只老鼠同时从A地到B地.老鼠见猫沿着大半圆行走,它不敢与猫同行(怕被猫吃掉),就沿着4个小半圆行走.假设猫和老鼠行走的速度相同,那么下列结论正确的是(C)
A. 猫先到达B地
B. 老鼠先到达B地
C. 猫和老鼠同时到达B地
D. 无法确定
(3)拓展:请仿照上面的探索方法和步骤,计算并推导出:当把大圆直径平均分成n等份时,以每条线段为直径画小圆,那么每个小圆的面积$S_{n}$与大圆的面积S之间的关系是$S_{n} = \frac{1}{n^{2}}S$.

答案： 解：
(1)② $\frac{1}{3}\pi a$；$\frac{1}{3}L$. ③ $\frac{1}{4}\pi a$；$\frac{1}{4}L$. ④ $\frac{1}{n}\pi a$；$\frac{1}{n}L$.
(2)C.
(3)$S_{n} = \frac{1}{n^{2}}S$.