《2025年课时A计划九年级数学上册人教版》

1.[与T5互为孪生题]如图,某学校拟建一块矩形花圃,打算一边利用学校现有的墙(墙足够长),其余三边除门外用栅栏围成,栅栏总长度为50m,门宽为2m,则这个矩形花圃的最大面积是(C)

A.169m²
B.288m²
C.338m²
D.312.5m²
【变式训练】(1)200 (2)10

答案： C 【变式训练】
(1)200
(2)10

[2024·合肥庐阳区二模]如图,某校师生要在空地上修建一个矩形劳动教育基地ABCD,该基地一边靠墙(墙长a m),另三边用总长40m的栅栏围成.
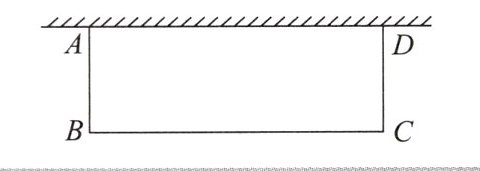
(1)当a= 25时,劳动教育基地的最大面积为$200m^2;$
(2)[选做题]当劳动教育基地的最大面积为$150m^2$时,a的值为$10.$

答案： 【解析】：
### $(1)$求当$a = 25$时劳动教育基地的最大面积
设$AB = xm$，则$BC=(40 - 2x)m$，设矩形$ABCD$的面积为$S m^2$。
根据矩形面积公式$S=AB\times BC$，可得$S=x(40 - 2x)=-2x^{2}+40x$。
对于二次函数$y = ax^{2}+bx + c$（$a\neq0$），这里$a=-2$，$b = 40$，$c = 0$，其对称轴为$x=-\frac{b}{2a}=-\frac{40}{2\times(-2)} = 10$。
因为$a=-2\lt0$，所以二次函数图象开口向下，在对称轴$x = 10$处取得最大值。
此时$BC=40-2x=40 - 2\times10 = 20m$，比较$20$与$25$的大小，$20\lt25$，满足墙长条件。
把$x = 10$代入$S=-2x^{2}+40x$，可得$S=-2\times10^{2}+40\times10=-200 + 400=200$。
### $(2)$求当最大面积为$150m^2$时$a$的值
由$S=-2x^{2}+40x$，当$S = 150$时，$-2x^{2}+40x=150$。
整理得$2x^{2}-40x + 150 = 0$，即$x^{2}-20x + 75 = 0$。
分解因式得$(x - 15)(x - 5)=0$，则$x - 15 = 0$或$x - 5 = 0$，解得$x_{1}=15$，$x_{2}=5$。
当$x = 15$时，$BC=40-2x=40-2\times15 = 10$；当$x = 5$时，$BC=40-2x=40 - 2\times5 = 30$。
因为当$x = 15$时，$BC = 10$；当$x = 5$时，$BC = 30$，而最大面积是$150m^2$，根据二次函数性质，此时$BC$的值要满足墙长条件，所以$a$的值为$10$。
【答案】：$(1)200$ $(2)10$

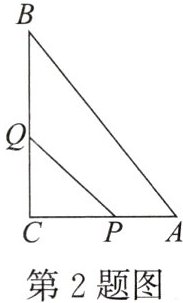
2.如图,在△ABC中,∠C= 90°,AB= 10cm,BC= 8cm,点P从点A出发沿AC向点C以1cm/s的速度运动,同时点Q从点C出发沿CB向点B以2cm/s的速度运动(点Q运动到点B时,两点同时停止运动).在运动过程中,△PCQ面积的最大值为(C)
A.24cm²
B.15cm²
C.9cm²
D.8cm²

答案： C

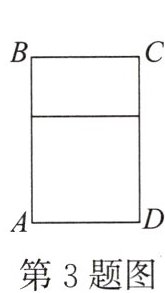
3.如图,用总长度为12m的铝合金材料做一个“日”字形的窗框ABCD,则做成的窗框的最大透光面积为(B)
A.4m²
B.6m²
C.12m²
D.16m²

答案： B 【变式训练】6

用总长为a m的材料做成如图1所示的“日”字形窗框,设窗框的宽为x m,窗框的面积为$y m^2,y$关于x的函数图象如图2所示,则a的值是______6.

答案： 【解析】：
设窗框的高为$h$，由“日”字形窗框可知，材料总长$a = 3x + 2h$，则$h=\dfrac{a - 3x}{2}$。
根据矩形面积公式$y = xh$，把$h=\dfrac{a - 3x}{2}$代入可得：$y=x\cdot\dfrac{a - 3x}{2}=-\dfrac{3}{2}x^{2}+\dfrac{a}{2}x$。
由二次函数$y = ax^{2}+bx + c$（$a\neq0$）的对称轴公式$x =-\dfrac{b}{2a}$，对于$y =-\dfrac{3}{2}x^{2}+\dfrac{a}{2}x$，其中$a =-\dfrac{3}{2}$，$b=\dfrac{a}{2}$，其对称轴为$x =-\dfrac{\dfrac{a}{2}}{2\times\left(-\dfrac{3}{2}\right)}=\dfrac{a}{6}$。
从图$2$可知，对称轴$x = 1$，所以$\dfrac{a}{6}=1$，解得$a = 6$。
【答案】：$6$

4.手工课上,小明准备做一个菱形的风筝,这个菱形的两条对角线长度之和恰好为60cm,菱形的面积$S(cm^2)$随其中一条对角线的长x(cm)的变化而变化.
(1)请直接写出S与x之间的函数关系式.
$S=-\frac {1}{2}x^{2}+30x$
(2)当x为多少时,菱形风筝的面积S最大?最大面积是多少?
当x为30时，菱形风筝的面积S最大，最大面积是$450cm^{2}$.
(3)请说明(1)中的函数S随x的变化情况.
当$0\lt x＜30$时，S随x的增大而增大；当$30\lt x＜60$时，S随x的增大而减小.

答案： 解：
(1)$S=\frac {1}{2}x(60-x)=-\frac {1}{2}x^{2}+30x$.
(2)当x为30时，菱形风筝的面积S最大，最大面积是$450cm^{2}$.
(3)当$0\lt x＜30$时，S随x的增大而增大；
当$30\lt x＜60$时，S随x的增大而减小.