第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
9. 已知函数:① $ y = 2 x - 1 $;② $ y = - 2 x ^ { 2 } - 1 $;③ $ y = 3 x ^ { 3 } - 2 x ^ { 2 } $;④ $ y = 2 ( x + 3 ) ^ { 2 } - 2 x ^ { 2 } $;⑤ $ y = a x ^ { 2 } + b x + c $;⑥ $ y = x ^ { 2 } + \frac { 1 } { x } + 5 $. 其中二次函数的个数为 (
A. 1
B. 2
C. 3
D. 4
A
)A. 1
B. 2
C. 3
D. 4
答案:
A
10. 如图是一个迷宫游戏盘的平面示意图,该矩形的长、宽分别为 5 cm,3 cm,其中阴影部分为迷宫的挡板,设挡板的宽度为 $ x $ cm,小球滚动的区域(空白区域)面积为 $ y \mathrm { cm } ^ { 2 } $,则 $ y $ 与 $ x $ 之间的函数关系式为 (
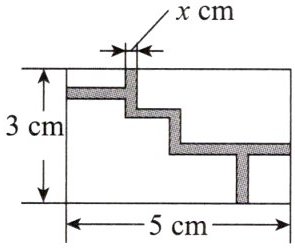
A. $ y = 2 x ^ { 2 } - 8 x + 15 $
B. $ y = x ^ { 2 } - 8 x + 15 $
C. $ y = x ^ { 2 } - 15 x + 8 $
D. $ y = 2 x ^ { 2 } - 15 x + 8 $
B
)
A. $ y = 2 x ^ { 2 } - 8 x + 15 $
B. $ y = x ^ { 2 } - 8 x + 15 $
C. $ y = x ^ { 2 } - 15 x + 8 $
D. $ y = 2 x ^ { 2 } - 15 x + 8 $
答案:
B
11. 已知函数 $ y = ( m ^ { 2 } - m ) x ^ { 2 } + ( m - 1 ) x + 2 - 2 m $.
(1)若这个函数是关于 $ x $ 的二次函数,则 $ m $ 的取值范围为
(2)若这个函数是关于 $ x $ 的一次函数,则 $ m $ 的值为
(3)这个函数
(1)若这个函数是关于 $ x $ 的二次函数,则 $ m $ 的取值范围为
$ m \neq 0 $ 且 $ m \neq 1 $
;(2)若这个函数是关于 $ x $ 的一次函数,则 $ m $ 的值为
0
;(3)这个函数
不可能
(填“可能”或“不可能”)是关于 $ x $ 的正比例函数.
答案:
(1) $ m \neq 0 $ 且 $ m \neq 1 $
(2) 0
(3) 不可能
(1) $ m \neq 0 $ 且 $ m \neq 1 $
(2) 0
(3) 不可能
12. [与 T6 互为孪生题]某商品的进价为 40 元/件,售价为 50 元/件,每个月可卖出 210 件. 如果售价超过 50 元/件但不超过 80 元/件,每上涨 1 元每月少卖 1 件;如果售价超过 80 元/件,每上涨 1 元每月少卖 3 件. 设该商品的售价为 $ x $ ( $ x $ 为整数)元/件,每月的销售量为 $ y $ ( $ y $ 为正整数)件.
(1)求 $ y $ 与 $ x $ 之间的函数解析式,并直接写出自变量 $ x $ 的取值范围;
(2)设每月的销售利润为 $ W $ 元,请直接写出 $ W $ 与 $ x $ 之间的函数解析式.
(1)求 $ y $ 与 $ x $ 之间的函数解析式,并直接写出自变量 $ x $ 的取值范围;
(2)设每月的销售利润为 $ W $ 元,请直接写出 $ W $ 与 $ x $ 之间的函数解析式.
答案:
解:
(1) $ y = \begin{cases} 260 - x & (50 < x \leq 80), \\ 420 - 3x & (80 < x < 140). \end{cases} $
(2) $ W = \begin{cases} -x^2 + 300x - 10400 & (50 < x \leq 80), \\ -3x^2 + 540x - 16800 & (80 < x < 140). \end{cases} $
(1) $ y = \begin{cases} 260 - x & (50 < x \leq 80), \\ 420 - 3x & (80 < x < 140). \end{cases} $
(2) $ W = \begin{cases} -x^2 + 300x - 10400 & (50 < x \leq 80), \\ -3x^2 + 540x - 16800 & (80 < x < 140). \end{cases} $
13. [教材 P41 习题 22.1 第 8 题改编]如图,正方形 $ A B C D $ 的边长为 4 cm,动点 $ P, Q $ 同时从点 $ A $ 出发,以 $ 1 \mathrm { cm } / \mathrm { s } $ 的速度分别沿 $ A \to B \to C $ 和 $ A \to D \to C $ 的路径向点 $ C $ 运动. 设运动时间为 $ x \mathrm { s } $,依次连接 $ P, B, D, Q $ 四点所围成的图形的面积为 $ y \mathrm { cm } ^ { 2 } $,求 $ y $ 关于 $ x ( 0 \leq x \leq 8 ) $ 的函数解析式.
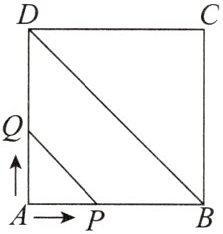
$ y = \begin{cases}

$ y = \begin{cases}
-\frac{1}{2}x^2 + 8
& (0 \leq x \leq 4), \\ -\frac{1}{2}x^2 + 8x - 24
& (4 < x \leq 8). \end{cases} $
答案:
解:$ y = \begin{cases} -\frac{1}{2}x^2 + 8 & (0 \leq x \leq 4), \\ -\frac{1}{2}x^2 + 8x - 24 & (4 < x \leq 8). \end{cases} $
查看更多完整答案,请扫码查看


