《2025年课时A计划九年级数学上册人教版》

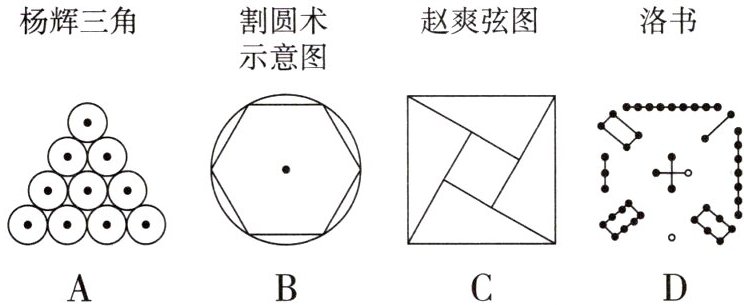
10.[数学文化]我国古代数学的发展历史源远流长,曾诞生了很多伟大的数学发现.下列与我国古代数学发现相关的图形中,既是轴对称图形,又是中心对称图形的是 (B)

答案： B

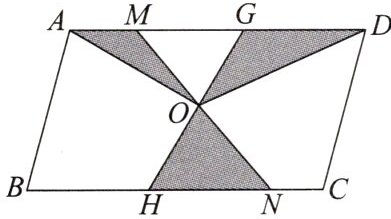
11.如图,点O是□ABCD的对称中心$,S_{□ABCD}= 24 cm^2,$线段GH和MN都经过点O,其中点M,G在AD上,点H,N在BC上.连接OA,OD,则图中阴影部分的面积为6cm^2.

答案： 6

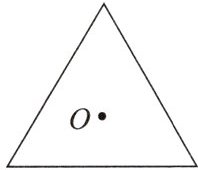
12.[核心素养——几何直观]如图是两张完全重合在一起的正三角形硬纸片,点O是它们的中心,若按住下面的纸片不动,将上面的纸片绕点O顺时针旋转,至少旋转60°的角后,两张硬纸片所构成的图形是中心对称图形.

答案： 60

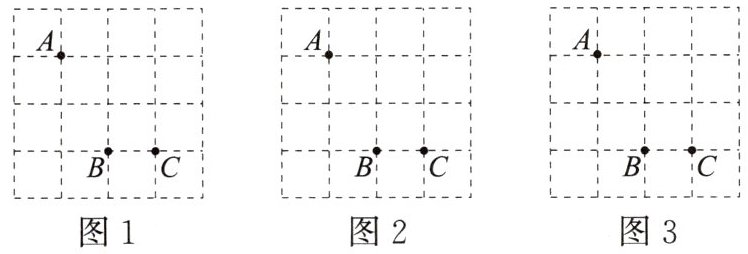
13.[开放题]如图,方格纸中有三个点A,B,C,要求作一个四边形使这三个点在这个四边形的边(包括顶点)上,且四边形的顶点在方格的顶点上.
(1)在图1中作出的四边形是中心对称图形但不是轴对称图形;
(2)在图2中作出的四边形是轴对称图形但不是中心对称图形;
(3)在图3中作出的四边形既是轴对称图形又是中心对称图形.

答案：
解:如图所示.(答案不唯一)
　 　　 　　

14.[教材P77复习题23第7题改编]知识背景:过中心对称图形的对称中心的任意一条直线都将其分成全等的两个部分.
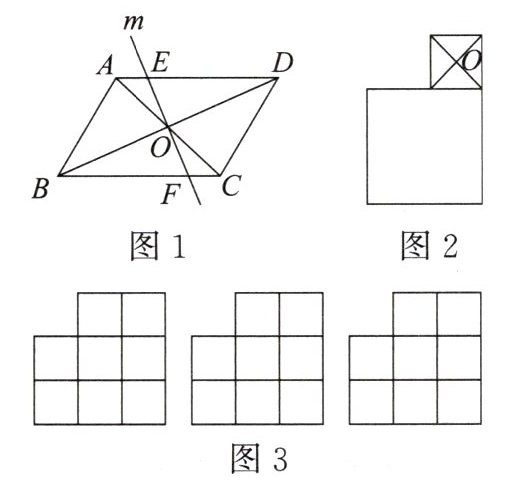
(1)如图1,直线m经过□ABCD对角线的交点O,则$S_{四边形AEFB}______S_{四边形CFED};($填“＞”“＜”或“=”)
(2)如图2,两个正方形如图所示摆放,O为小正方形对角线的交点,作过点O的直线将整个图形分成面积相等的两部分;
(3)八个大小相同的正方形如图3所示摆放,作直线将整个图形分成面积相等的两部分.(用三种方法分割)

答案：
解:
(1)=.
(2)如图1所示.
(3)如图2所示.(答案不唯一，合理即可)