《2025年课时A计划九年级数学上册人教版》

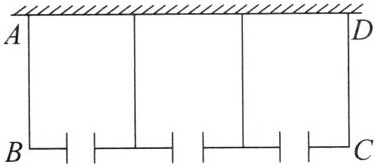
5. [与T3互为孪生题]如图,用一段77米长的篱笆围成三个一边靠墙、大小相同的矩形羊圈,每个矩形羊圈都有一扇1米宽的门,墙的最大可用长度为30米.如果羊圈的总面积为300米$^2,$则边AB的长为(C)

A. 5
B. 10
C. 15
D. 20

答案： C

6. [2024·合肥蜀山区期末]为了节省材料,某农场水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为120米的围网在水库中围成了如图所示的①②③三块长方形区域,且这三块长方形区域的面积都为225米$^2,$则图中区域①长方形的长a为30米.

答案： 30

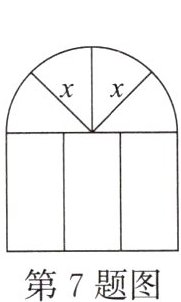
7. [易错题]某建筑物的窗户如图所示,它的上半部分是半径为x米的半圆,下半部分是长方形,制造窗框的材料总长(图中所有黑线的长度和)为15米.当x等于1或$\frac{8}{7}$米时,窗户的总透光面积是4米$^2.$

答案： 1或$\frac{8}{7}$

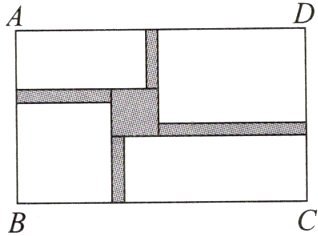
8. [2024·合肥瑶海区期末]有一个长、宽分别为20m和12m的长方形水池ABCD,某旅游景点要在水池中建一个与长方形的边互相平行的正方形观赏亭和连接观赏亭的四条道路,如图所示,道路的宽度相等,其中两条与AB平行,另两条与BC平行,已知道路的宽为正方形边长的$\frac{1}{4}$,若道路与观赏亭的面积之和是原长方形水池面积的$\frac{1}{6}$.
(1)设道路的宽为xm,则正方形的面积为______16x²m²;(用含x的代数式表示)
(2)根据题中所给的信息列方程求道路的宽.

答案： 解：
(1)$16x^{2}$.
(2)依题意，得$x(20 - 4x) + x(12 - 4x) + (4x)^{2} = \frac{1}{6}×20×12$，
整理得$x^{2} + 4x - 5 = 0$，
解得$x_{1} = 1$，$x_{2} = -5$(不合题意，舍去).
答：道路的宽为1m.

9. 如图,在矩形ABCD中,AB= 6cm,AD= 2cm,点P以2cm/s的速度从点A出发沿折线A-B-C向点C运动,同时点Q以1cm/s的速度从点C出发向点D运动,当其中一个动点到达终点时,另一个动点也停止运动.
(1)经过多长时间,四边形PBCQ的面积是矩形ABCD面积的$\frac{4}{9}$? $\frac{2}{3}$s
(2)问两个动点在运动过程中是否存在某一时刻,使得点P与点Q之间的距离为$\sqrt{5}$cm?若存在,求运动所需的时间;若不存在,请说明理由. 存在，运动所需时间为$\frac{5}{3}$s或$\frac{7}{3}$s

答案： 解：
(1)经过$\frac{2}{3}$s，四边形PBCQ的面积是矩形ABCD面积的$\frac{4}{9}$.
(2)存在.
当运动$\frac{5}{3}$s或$\frac{7}{3}$s时，点P与点Q之间的距离为$\sqrt{5}$cm.