第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 下列现象不是旋转的是 (
A. 飞速转动的电风扇
B. 传送带传送货物
C. 时钟上指针的运动
D. 汽车方向盘的转动
B
)A. 飞速转动的电风扇
B. 传送带传送货物
C. 时钟上指针的运动
D. 汽车方向盘的转动
答案:
B
2. [教材P59练习第2题改编]李明家有一个时钟,国庆期间,某天上午他8点整出门锻炼,回家时发现时针刚好旋转了$60^{\circ }$,那么李明回家的时间是 (
A. 9点整
B. 9点半
C. 10点整
D. 10点半
C
)A. 9点整
B. 9点半
C. 10点整
D. 10点半
答案:
C
3. [与T9互为孪生题]如图,将$\triangle ABC$绕点A旋转至$\triangle ADE$,则旋转角是
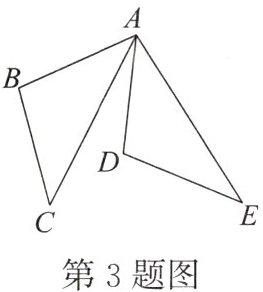
$\angle BAD$(或$\angle CAE$)
.(填一个即可)
答案:
$\angle BAD$(或$\angle CAE$)
4. 如图所示,AC是正方形ABCD的对角线,$\triangle ABC经过旋转后到达\triangle AEF$的位置,则旋转中心是点
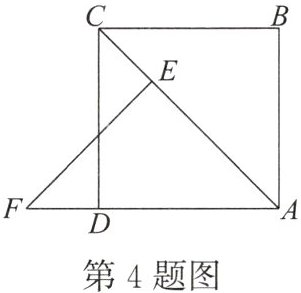
A
,旋转方向是逆时针
,旋转角度是$45^{\circ}$
,点C的对应点是点F
,BC的对应线段是EF
,$∠B$的对应角是$\angle AEF$
.
答案:
A 逆时针 $45^{\circ}$ F EF $\angle AEF$
5. [情境题]在体育课上,当老师下达口令“向左转”时,左脚正确的动作应是以
脚跟
为旋转中心,沿着逆时针
方向旋转90
°.
答案:
脚跟 逆时针 90
6. 如图,将$\triangle ABC$绕点C逆时针旋转$60^{\circ }得到\triangle A'B'C$,点A在边$B'C$上,则$∠A'CB$的度数是 (
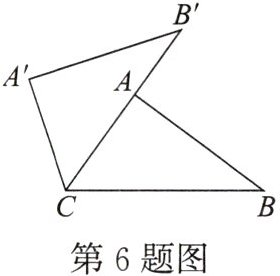
A. $60^{\circ }$
B. $90^{\circ }$
C. $110^{\circ }$
D. $120^{\circ }$
D
)
A. $60^{\circ }$
B. $90^{\circ }$
C. $110^{\circ }$
D. $120^{\circ }$
答案:
D
7. 如图,在△ABC中,∠C=90°,将△ABC绕点A按顺时针方向旋转,使点B落在点D处,点C落在AB边上的点E处,连接BD.若AC=4,BC=3,则线段BE的长为 (
A. $\sqrt {10}$
B. 2
C. 1
D. $\frac {1}{2}$
变式训练
题目条件不变,则线段BD的长为
C
)A. $\sqrt {10}$
B. 2
C. 1
D. $\frac {1}{2}$
变式训练
题目条件不变,则线段BD的长为
$\sqrt{10}$
.
答案:
C
@@$\sqrt{10}$
@@$\sqrt{10}$
8. [教材P76复习题23第5题改编]如图,C是线段AB上一点,分别以AC,BC为边,在AB的同侧作等边$\triangle ACD和等边\triangle BCE$,连接AE,BD交于点O.
(1)将$\triangle ACE$以点C为旋转中心顺时针旋转
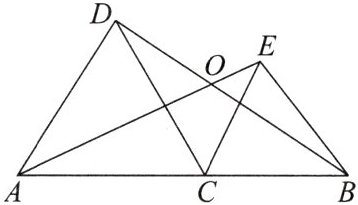
$60^{\circ }$后得到的三角形是图中的____
(2)求$∠AOD$的度数.
(1)将$\triangle ACE$以点C为旋转中心顺时针旋转

$60^{\circ }$后得到的三角形是图中的____
$\triangle DCB$
;(2)求$∠AOD$的度数.
$60^{\circ }$
答案:
解:
(1)$\triangle DCB$.
(2)由
(1)可知$\triangle ACE \cong \triangle DCB$,
$\therefore \angle DBC = \angle AEC$,
$\therefore \angle AOD = \angle BOE = \angle BCE = 60^{\circ}$.
(1)$\triangle DCB$.
(2)由
(1)可知$\triangle ACE \cong \triangle DCB$,
$\therefore \angle DBC = \angle AEC$,
$\therefore \angle AOD = \angle BOE = \angle BCE = 60^{\circ}$.
查看更多完整答案,请扫码查看


