《2025年课时A计划九年级数学上册人教版》

1.[与T8互为孪生题][2024·牡丹江中考]一种药品原价每盒48元,经过两次降价后每盒27元,两次降价的百分率相同,则每次降价的百分率为(C)
A.20%
B.22%
C.25%
D.28%

答案： C

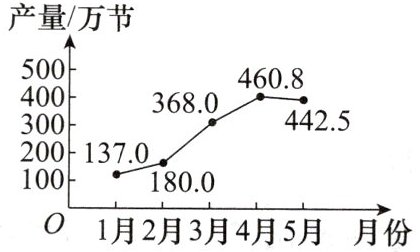
2.某电池厂2025年1~5月份的电池产量如图所示.设从2月份到4月份,该厂电池产量的月平均增长率为x,则x=60%

答案： 60%

3.某校为响应全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆128人次,进馆人次逐月增加,到第三个月末累计进馆608人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率.
(2)因条件限制,学校图书馆每月接纳能力不超过500人次,在进馆人次的月平均增长率不变的条件下,学校图书馆能否接纳第四个月的进馆人次?并说明理由.

答案： 解：
(1)设进馆人次的月平均增长率为x.
由题意，得$128 + 128(1 + x) + 128(1 + x)^2 = 608.$整理，得4x² + 12x - 7 = 0.
解得x₁ = 0.5 = 50%，x₂ = -3.5(舍去).
答：进馆人次的月平均增长率为50%.
(2)能.
理由：因为进馆人次的月平均增长率为50%，
所以第四个月的进馆人次为128×(1 + 50%)³ = 432，又因为432 ＜ 500，
所以学校图书馆能接纳第四个月的进馆人次.

4.某宾馆有50间房供游客居住,当每间房每天定价为180元时,宾馆会住满;当每间房每天的定价每增加10元时,就会空闲一间房.如果有游客居住,宾馆需对居住的每间房每天支出20元的费用.设房价定价为x元时,宾馆当天的利润为10890元,则可列方程为$(x - 20)(50 - \frac{x - 180}{10}) = 10890$.

答案： $(x - 20)(50 - \frac{x - 180}{10}) = 10890$

5.某广场从6月份开始对部分商品进行"折上折"(两次打折数相同)优惠活动,已知一件原价1000元的服装,优惠后实际仅需640元,则该服装原本打8折.

答案： 8

6.一种服装的进价为100元/件,经市场调查发现该服装若销售价为x元/件,则年销售量为(1000-2x)件.销售这种服装的员工每年工资等其他费用总计40000元.
(1)用含x的代数式表示每年销售这种服装的获利金额;
(2)若希望该服装一年的获利金额为32800元,且使产品年销售量较大,你认为销售价应定为多少元/件?

答案： 【解析】：
1. 首先明确获利金额的计算方法，获利金额等于每件服装的利润乘以年销售量再减去其他费用。每件服装的利润为销售价$x$元减去进价$100$元，即$(x - 100)$元，年销售量为$(1000 - 2x)$件，其他费用为$40000$元。所以每年销售这种服装的获利金额$y=(x - 100)(1000 - 2x)-40000$，展开式子：
根据多项式乘法法则$(a + b)(c + d)=ac+ad+bc+bd$，$(x - 100)(1000 - 2x)=x\times1000-x\times2x-100\times1000 + 100\times2x=1000x-2x^{2}-100000 + 200x=-2x^{2}+1200x - 100000$。
则$y=-2x^{2}+1200x - 100000-40000=-2x^{2}+1200x - 140000$。
2. 当获利金额$y = 32800$元时，即$-2x^{2}+1200x - 140000 = 32800$。
移项化为一元二次方程的一般形式：$-2x^{2}+1200x - 140000 - 32800 = 0$，即$-2x^{2}+1200x - 172800 = 0$。
两边同时除以$-2$得：$x^{2}-600x + 86400 = 0$。
对于一元二次方程$ax^{2}+bx + c = 0(a\neq0)$，这里$a = 1$，$b=-600$，$c = 86400$，根据求根公式$x=\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}$，先计算判别式$\Delta=b^{2}-4ac=(-600)^{2}-4\times1\times86400=360000 - 345600 = 14400$。
则$x=\frac{600\pm\sqrt{14400}}{2}=\frac{600\pm120}{2}$。
当取$+$号时，$x_{1}=\frac{600 + 120}{2}=\frac{720}{2}=360$；当取$-$号时，$x_{2}=\frac{600 - 120}{2}=\frac{480}{2}=240$。
3. 然后比较两种销售价下的年销售量：
当$x = 360$时，年销售量为$1000-2x=1000-2\times360=1000 - 720 = 280$件。
当$x = 240$时，年销售量为$1000-2x=1000-2\times240=1000 - 480 = 520$件。
因为$520＞280$，要使产品年销售量较大，所以销售价应定为$240$元/件。
【答案】：1. $-2x^{2}+1200x - 140000$ 2. $240$