《2025年课时A计划九年级数学上册人教版》

6. 小燕去参观一个蔬菜大棚,大棚横截面为抛物线,有关数据如图所示.已知小燕的身高为1.40米,在她不弯腰的情况下,横向活动范围有6米.

答案： 6

7. [情境题][2024·淮南期中]我们常见的炒菜锅和锅盖都是抛物线面,经过锅心和盖心的纵断面是两段抛物线组合而成的封闭图形,不妨简称为“锅线”.现有一炒菜锅锅口直径为6dm,锅深3dm,锅盖高1dm(锅口直径与锅盖直径视为相同),建立平面直角坐标系如图所示,把锅纵断面的抛物线记为$ C _ { 1 } $,把锅盖纵断面的抛物线记为$ C _ { 2 } $.

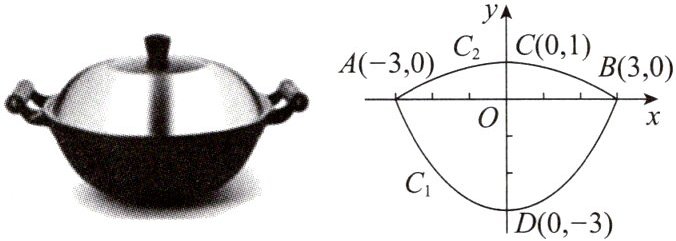
(1)求$ C _ { 1 } $和$ C _ { 2 } $的解析式;
$ C _ { 1 } $的解析式为$ y = \frac { 1 } { 3 } x ^ { 2 } - 3 ( - 3 \leq x \leq 3 ) $，$ C _ { 2 } $的解析式为$ y = - \frac { 1 } { 9 } x ^ { 2 } + 1 ( - 3 \leq x \leq 3 ) $.
(2)如果将一个底面直径为2dm、高度为3.6dm的圆柱形器皿竖直放入炒菜锅内蒸食物,锅盖能否正常盖上? 请说明理由.
锅盖不能正常盖上.
理由：当 $ x = 1 $ 时，$ C _ { 1 } : y = \frac { 1 } { 3 } × 1 ^ { 2 } - 3 = - \frac { 8 } { 3 } $，
$ C _ { 2 } : y = - \frac { 1 } { 9 } × 1 ^ { 2 } + 1 = \frac { 8 } { 9 } $，
$ \because \frac { 8 } { 9 } - \left( - \frac { 8 } { 3 } \right) = \frac { 32 } { 9 } ＜ 3.6 $，∴锅盖不能正常盖上.

答案： 解：
(1)$ C _ { 1 } $ 的解析式为 $ y = \frac { 1 } { 3 } x ^ { 2 } - 3 ( - 3 \leq x \leq 3 ) $，
$ C _ { 2 } $ 的解析式为 $ y = - \frac { 1 } { 9 } x ^ { 2 } + 1 ( - 3 \leq x \leq 3 ) $.
(2)锅盖不能正常盖上.
理由：当 $ x = 1 $ 时，$ C _ { 1 } : y = \frac { 1 } { 3 } \times 1 ^ { 2 } - 3 = - \frac { 8 } { 3 } $，
$ C _ { 2 } : y = - \frac { 1 } { 9 } \times 1 ^ { 2 } + 1 = \frac { 8 } { 9 } $，
$ \because \frac { 8 } { 9 } - \left( - \frac { 8 } { 3 } \right) = \frac { 32 } { 9 } ＜ 3.6 $，
∴锅盖不能正常盖上.

8. [项目式学习][项目主题]怎样才能命中篮筐
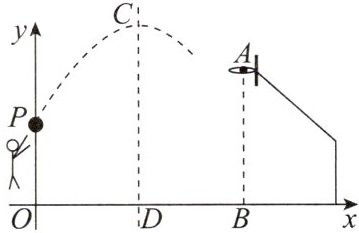
[项目背景]学校组织班级间篮球比赛,小明发现自己投篮命中率较低,特请同学小红拍摄自己投篮图片,并测量相应的数据进行研究.
[模型建立]如图建立平面直角坐标系,篮球运动轨迹可以看作是抛物线的一部分.
素材1:在初次投篮时,小红测得$ O P = 2.2 $米,篮筐高$ A B = 3 $米,$ O B = 6 $米,篮球距离地面的最大高度$ C D = 4 $米,此时$ O D = 3 $米.
素材2:当篮球P恰好经过篮筐中心点A时,我们称此次进球为“空心球”.已知篮球的高度y(米)满足$ 2.95 \leqslant y \leqslant 3.10 $时,篮球可命中篮筐.(小明在投篮过程中始终保持投篮方向和出手速度不变)
[解决问题]
(1)小明初次投篮时____不能命中篮筐.(填“能”或“不能”)
(2)小红对小明的初次投篮数据进行研究后,让小明在原来位置向前走了t米后再次投篮,发现正好投进一个“空心球”,求t的值.(保留根号)
(3)在比赛过程中,小明在离篮筐中心的水平距离5米处开始起跳投篮,能否命中篮筐? 如果不能,那么要想命中篮筐,篮球的出手点高度c的取值范围是多少?

答案： 解：
(1)不能.
(2)由
(1)可设向前走了 $ t $ 米后抛物线的解析式为
$ y = - \frac { 1 } { 5 } ( x - 3 - t ) ^ { 2 } + 4 $.
把点 $ ( 6, 3 ) $ 代入，得 $ 3 = - \frac { 1 } { 5 } ( 6 - 3 - t ) ^ { 2 } + 4 $，
解得 $ t _ { 1 } = 3 + \sqrt { 5 } $（不合题意，舍去），$ t _ { 2 } = 3 - \sqrt { 5 } $.
(3)$ 1.95 \leq c \leq 2.1 $.