《2025年课时A计划九年级数学上册人教版》

7. [2024·合肥蜀山区校级期中]《中华人民共和国道路交通安全法》规定,同车道行驶的机动车,后车应当与前车保持足以采取紧急制动措施的安全距离,其原因可以用物理和数学的知识来解释. 公路上行驶的汽车急刹车时,刹车距离s(m)与时间t(s)的函数关系式为$s= 16t-4t^{2}$,当遇到紧急情况刹车时,后车应当与前车保持足以采取紧急制动措施的最小安全距离为(D)
A. 13 m
B. 14 m
C. 15 m
D. 16 m

答案： D

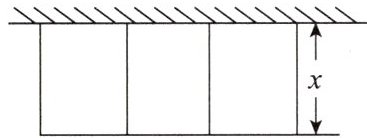
8. 如图,某农场计划修建三间矩形饲养室,饲养室一面靠现有墙(墙可用长$\leqslant 20m$),中间用两道墙隔开. 已知计划中的修筑材料可建围墙总长为60m,设饲养室宽为xm,占地总面积为$ym^{2}$,则三间饲养室总面积的最大值为$ 200 \mathrm { m } ^ { 2 } $.

答案： $ 200 \mathrm { m } ^ { 2 } $

9. 某高档游泳健身馆每人每次游泳健身的票价为80元,每日平均客流量为136人. 为了促进全民健身运动,游泳馆决定降价促销,经市场调查发现,票价每下降1元,每日游泳健身的人数平均增加2人. 当票价下降6元时,每日销售收入最大.

答案： 6

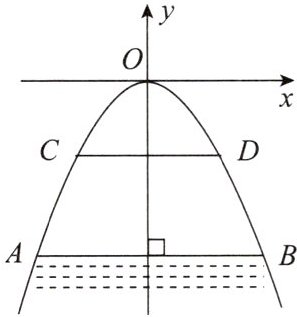
10. 如图,有一座抛物线形拱桥,桥下面在正常水位AB时,水面宽度为20米,水面距离拱顶4米,当水位上升达到警戒线CD时,水面宽度为10米. 若洪水到来时,水位以每小时0.2米的速度从警戒线开始上升,则再持续5小时才能到拱桥顶.

答案： 5

11. [综合与实践]【主题】优化洒水车为公路两侧绿化带浇水效率
【问题背景】如图1,洒水车沿着平行于公路绿化带方向行驶,同时向右侧绿化带浇水. 某数学兴趣小组想了解洒水车要如何控制行驶路线与绿化带之间的距离,才能保证喷出的水能浇灌到整个绿化带,于是建立数学模型进行探索.
【数学建模】如图2建立平面直角坐标系,可以把洒水车喷出水的内、外边缘抽象为两条抛物线. 喷水口的竖直高度OH为1.5m,绿化带横截面是矩形DEFG,且$DE= 3m$,$EF= 0.5m$. 内边缘抛物线$y_{2}是由外边缘抛物线y_{1}$向左平移得到,且抛物线$y_{1}$的最高点A与喷水口的水平距离为2m,与喷水口的竖直距离为0.5m.

【解决问题】
(1)求外边缘抛物线$y_{1}$的解析式,并求喷出水的最大射程OC；
解：外边缘抛物线的解析式为$ y _ { 1 } = - \frac { 1 } { 8 } ( x - 2 ) ^ { 2 } + 2 $；喷出水的最大射程 $ OC $ 为$ 6 \mathrm { m } $.
(2)请求出内边缘抛物线$y_{2}$与x轴的正半轴交点B的坐标；
解：点 $ B $ 的坐标为$ ( 2,0 ) $.
(3)要使洒水车行驶时喷出的水能浇灌到整个绿化带,请直接写出OD的取值范围.
解：OD的取值范围为$ 2 \leq O D \leq 2 \sqrt { 3 } - 1 $.

答案： 解：
(1)外边缘抛物线的解析式为 $ y _ { 1 } = - \frac { 1 } { 8 } ( x - 2 ) ^ { 2 } + 2 $；喷出水的最大射程 $ OC $ 为 $ 6 \mathrm { m } $.
(2)点 $ B $ 的坐标为 $ ( 2,0 ) $.
(3) $ 2 \leq O D \leq 2 \sqrt { 3 } - 1 $.