《2025年课时A计划九年级数学上册人教版》

1. 某种商品每天的销售利润y(元)与单价x(元)之间的函数关系式为$y= -0.1(x-3)^{2}+25$,则这种商品每天的最大销售利润为 (C)
A. 0.1元
B. 3元
C. 25元
D. 75元

答案： C

2. [2023·芜湖无为期中]某超市销售某款商品每天的销售利润y(元)与单价x(元)之间的函数关系式为$y= -x^{2}+10x+125$,则销售这款商品每天的最大利润为150元.

答案： 150

3. [教材P51习题22.3第2题改编]某种商品每件进价为18元,调查表明:在某段时间内若以每件x元$(18≤x≤30$,且x为整数)出售,可卖出$(30-x)$件,要使利润最大,则每件商品的售价应为 (D)
A. 18元
B. 20元
C. 22元
D. 24元

答案： D

4. 某品牌钢笔进价为8元/支,按10元/支出售时每天能卖出20支.市场调查发现如果每支每涨价1元,每天就少卖出2支,为了每天获得最大利润,其售价应定为14元/支.

答案： 14

通过涨价获取利润→通过降价获取利润
某旅行社组团去外地旅游,30人起组团,每人价格800元.旅行社对超过30人的团给予优惠,即旅行团的人数每增加1人,每人的价格就降低10元(单价不低于500元).当一个旅行团的人数为55时,这个旅行社可以获得最大营业额.

答案： 【变式训练】55

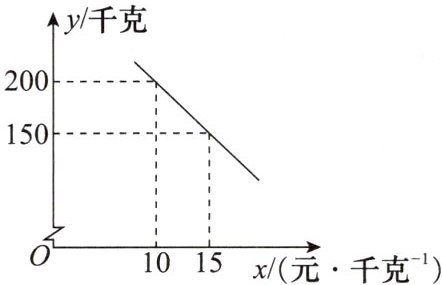
5. 某乡镇实施产业扶贫,帮助贫困户承包荒山种植蜜柚.到了收获季节,已知该蜜柚的成本价为8元/千克,投入市场销售时,调查市场行情,发现该蜜柚销售不会亏本,且每天销量y(千克)与销售单价x(元/千克)之间的函数关系如图所示.当该蜜柚定价为19元/千克时,每天销售获得的利润最大,最大利润是1210元.

答案： 19 1210

6. [2024·合肥蜀山区期末]某公司生产一种产品,生产费用y(万元)由制造费用、材料费用和人工费用三部分组成.已知该公司每年生产该产品x件,制造费用为$y_{1}$(万元),材料费用为$y_{2}$(万元),人工费用为固定费用1000万元,其中$y_{1}= ax^{2}$,$y_{2}= bx$,生产时得到了表中的数据.

(1)求y与x的函数解析式;$y=\frac{1}{10}x^{2}+5x+1000$
(2)公司每年生产的该产品均全部售出,经市场调查,产品的销售单价p(万元/件)与生产件数x(件)满足一次函数关系$p= 45-\frac {1}{30}x$.设该产品每年的利润为w万元(利润= 销售收入-生产费用),求w的最大值.2000

答案： 解：
(1)y与x的函数解析式为$y=\frac{1}{10}x^{2}+5x+1000$。
(2)由题意得$w=(45-\frac{1}{30}x)x-(\frac{1}{10}x^{2}+5x+1000)=45x-\frac{1}{30}x^{2}-\frac{1}{10}x^{2}-5x-1000=-\frac{2}{15}x^{2}+40x-1000=-\frac{2}{15}(x-150)^{2}+2000$，
$\because -\frac{2}{15}＜0$，
∴当$x=150$时，w最大，最大值为2000。