第50页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 如图是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为 (
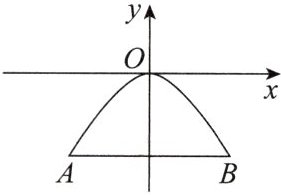
【变式训练】(
A. $ y = \frac { 25 } { 4 } x ^ { 2 } $
B. $ y = - \frac { 25 } { 4 } x ^ { 2 } $
C. $ y = - \frac { 4 } { 25 } x ^ { 2 } $
D. $ y = \frac { 4 } { 25 } x ^ { 2 } $
C
)
【变式训练】(
A
)A. $ y = \frac { 25 } { 4 } x ^ { 2 } $
B. $ y = - \frac { 25 } { 4 } x ^ { 2 } $
C. $ y = - \frac { 4 } { 25 } x ^ { 2 } $
D. $ y = \frac { 4 } { 25 } x ^ { 2 } $
答案:
C 【变式训练】A
已建坐标系→未建坐标系
如图,一拱桥呈抛物线形状,桥的最大高度CM是16米,跨度AB是40米,则在线段AB上离中心M点5米处的地方,桥的高度是
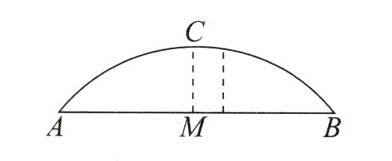
(
A. 15米
B. 14米
C. 13米
D. 12米
如图,一拱桥呈抛物线形状,桥的最大高度CM是16米,跨度AB是40米,则在线段AB上离中心M点5米处的地方,桥的高度是

(
C
)A. 15米
B. 14米
C. 13米
D. 12米
答案:
C 【变式训练】A
2. 如图是丁丁设计的一款杯子的平面图,建立平面直角坐标系后杯子的上半部分是二次函数$ y = 2 x ^ { 2 } + 8 $的图象的一部分.若$ A B = 4 $,$ D E = 3 $,则杯子的高CE为
11
.
答案:
11
3. [易错题]小明在进行物理实验时竖直向上抛出一个小球,小球上升的高度h(m)与运动时间t(s)的函数关系式为$ h = a t ^ { 2 } + b t $,图象如图所示.若小球在抛出后第2s与第6s时的高度相等,则下列时刻中小球的高度最高的是 (
A. 第3s
B. 第3.9s
C. 第4.5s
D. 第6.5s
B
)A. 第3s
B. 第3.9s
C. 第4.5s
D. 第6.5s
答案:
B
4. 某水幕是由若干个水嘴喷出的水柱组成的(如图),水柱的最高点为P,$ O B = 2 m $,$ B P = 10 m $,水嘴高$ O D = 6 m $,则图中抛物线的解析式为
$ y = - ( x - 2 ) ^ { 2 } + 10 $
.(不要求化成一般形式)
答案:
$ y = - ( x - 2 ) ^ { 2 } + 10 $
5. [2024·合肥包河区期末]足球训练中球员从球门正前方9m的A处射门,球射向球门的路线呈抛物线.当球飞行至与球门水平距离3m处时,球达到最高点,此时球离地面3m.现以O为原点建立如图所示的平面直角坐标系.
(1)求抛物线的解析式;
(2)已知球门高OB为2.44m,通过计算判断球能否射进球门(忽略其他因素).
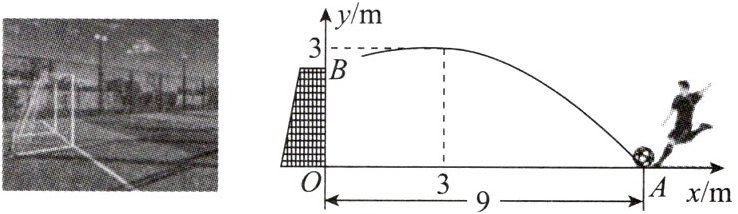
(1)求抛物线的解析式;
$ y = - \frac { 1 } { 12 } ( x - 3 ) ^ { 2 } + 3 $
(2)已知球门高OB为2.44m,通过计算判断球能否射进球门(忽略其他因素).
能

答案:
解:
(1)抛物线的解析式为 $ y = - \frac { 1 } { 12 } ( x - 3 ) ^ { 2 } + 3 $.
(2)当 $ x = 0 $ 时,$ y = - \frac { 1 } { 12 } \times 9 + 3 = \frac { 9 } { 4 } < 2.44 $,
∴球能射进球门.
(1)抛物线的解析式为 $ y = - \frac { 1 } { 12 } ( x - 3 ) ^ { 2 } + 3 $.
(2)当 $ x = 0 $ 时,$ y = - \frac { 1 } { 12 } \times 9 + 3 = \frac { 9 } { 4 } < 2.44 $,
∴球能射进球门.
查看更多完整答案,请扫码查看


