第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
1. 将△AOB绕点O旋转180°得到△DOE,则下列作图正确的是 (

C
)
答案:
C
2. 在图中作出“三角旗”绕点O顺时针旋转90°后的图案.


按照旋转性质,先确定三角旗各顶点绕点O顺时针旋转90°后的位置,再依次连接这些顶点得到旋转后的图案
答案:
【解析】:根据旋转的性质,图形绕点$O$顺时针旋转$90^{\circ}$,就是将三角旗的每条边绕点$O$顺时针旋转$90^{\circ}$。先确定三角旗的几个顶点绕点$O$顺时针旋转$90^{\circ}$后的位置,再依次连接这些顶点。
【答案】:按照上述方法画出旋转后的图案(由于无法直接绘制图形,学生可根据旋转规则自行绘制)。
【答案】:按照上述方法画出旋转后的图案(由于无法直接绘制图形,学生可根据旋转规则自行绘制)。
3. [2024·合肥庐江期末节选]如图,在8×6的长方形网格中,每个小正方形的边长都为1个单位长度,我们把每个小正方形的顶点称为格点,A,B,C均为格点.请你用一把无刻度的直尺完成作图,并保留作图痕迹.
(1)以点C为旋转中心,将线段AC逆时针旋转90°至线段CD,连接AD;
(2)过点C作CE⊥AD于点E.

(1)以点C为旋转中心,将线段AC逆时针旋转90°至线段CD,连接AD;
按照利用网格特点构造全等直角三角形的方法作出线段CD并连接AD(具体作图痕迹根据网格实际操作呈现)
(2)过点C作CE⊥AD于点E.
按照利用网格中正方形对角线互相垂直的性质作出CE⊥AD于点E(具体作图痕迹根据网格实际操作呈现)

答案:
【解析】:
(1) 利用网格特点,通过构造全等的直角三角形来确定点$D$的位置。因为要将线段$AC$逆时针旋转$90^{\circ}$至线段$CD$,所以过点$C$作与$AC$垂直且长度相等的线段$CD$(利用格点构造直角,使直角边分别与$AC$在水平和垂直方向的长度对应相等),然后连接$AD$。
(2) 利用网格中正方形的对角线互相垂直的性质。找到与$AD$相关的正方形对角线,通过平移等方式确定$CE$的位置,使得$CE\perp AD$。
【答案】:
(1) 按照上述方法作出线段$CD$并连接$AD$(具体作图痕迹根据网格实际操作呈现)。
(2) 按照上述方法作出$CE\perp AD$于点$E$(具体作图痕迹根据网格实际操作呈现)。
(1) 利用网格特点,通过构造全等的直角三角形来确定点$D$的位置。因为要将线段$AC$逆时针旋转$90^{\circ}$至线段$CD$,所以过点$C$作与$AC$垂直且长度相等的线段$CD$(利用格点构造直角,使直角边分别与$AC$在水平和垂直方向的长度对应相等),然后连接$AD$。
(2) 利用网格中正方形的对角线互相垂直的性质。找到与$AD$相关的正方形对角线,通过平移等方式确定$CE$的位置,使得$CE\perp AD$。
【答案】:
(1) 按照上述方法作出线段$CD$并连接$AD$(具体作图痕迹根据网格实际操作呈现)。
(2) 按照上述方法作出$CE\perp AD$于点$E$(具体作图痕迹根据网格实际操作呈现)。
4. [情境题]在俄罗斯方块游戏中,已拼好的图案如图所示,现又出现一方格体正在向下运动,为了使所有图案消失,必须进行以下哪项操作,才能拼成一个完整图案,使其自动消失 (
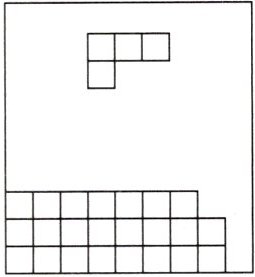
A. 顺时针旋转90°,向右平移
B. 逆时针旋转90°,向右平移
C. 顺时针旋转90°,向左平移
D. 逆时针旋转90°,向左平移
A
)
A. 顺时针旋转90°,向右平移
B. 逆时针旋转90°,向右平移
C. 顺时针旋转90°,向左平移
D. 逆时针旋转90°,向左平移
答案:
A
5. [教材P63习题23.1第6题改编]若正八边形绕它的中心旋转一定角度后能与自身完全重合,则其旋转的角度至少为
方法总结
任何正n边形绕其中心旋转$\frac {360^{\circ }}{n}$即可与自身重合.
45°
.方法总结
任何正n边形绕其中心旋转$\frac {360^{\circ }}{n}$即可与自身重合.
答案:
$45^{\circ}$
6. [新考向—无刻度直尺作图][教材P60例题改编]已知正方形ABCD,E为BC的中点,F为CD的中点,请仅用无刻度直尺按要求完成以下作图.(保留作图痕迹,不写作法)
(1)如图1,连接AF,将△ADF绕点D逆时针旋转90°,画出旋转后的三角形.
(2)如图2,连接BF,将△BCF绕点C顺时针旋转90°,画出旋转后的三角形.
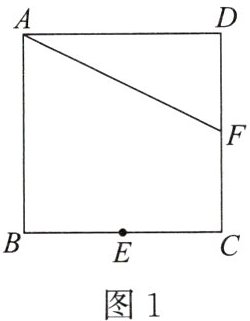

(1)如图1,连接AF,将△ADF绕点D逆时针旋转90°,画出旋转后的三角形.
(2)如图2,连接BF,将△BCF绕点C顺时针旋转90°,画出旋转后的三角形.


答案:
解:
(1)如图 1 所示,$\triangle CDF_1$ 即为所求.
(2)如图 2 所示,$\triangle DCF_2$ 即为所求.


解:
(1)如图 1 所示,$\triangle CDF_1$ 即为所求.
(2)如图 2 所示,$\triangle DCF_2$ 即为所求.


查看更多完整答案,请扫码查看


