2025年1课3练江苏人民出版社八年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1课3练江苏人民出版社八年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第9页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
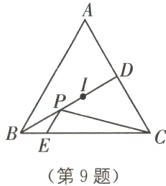
9(2024·内江中考)如图,在△ABC中,∠ABC = 60°,BC = 8,E是BC边上一点,且BE = 2,点I是△ABC的内心,BI的延长线交AC于点D,P是BD上一动点,连接PE,PC,则PE + PC的最小值为________.

答案:
9. $2\sqrt{13}$ [解析]如图,在AB上取点F,使BF = BE = 2,连接PF,CF,过点F作FH⊥BC于点H。
∵点I是△ABC的内心,
∴BI平分∠ABC,
∴∠ABD = ∠CBD。
又BP = BP,
∴△BFP≌△BEP(SAS),
∴PF = PE,
∴PE + PC = PF + PC≥CF,
∴当C,P,F三点共线时,PE + PC最小,最小值为CF的长。
∵FH⊥BC,∠ABC = 60°,
∴∠BFH = 30°,
∴BH = $\frac{1}{2}BF = 1$,
∴在Rt△BFH中,FH = $\sqrt{BF^{2}-BH^{2}}=\sqrt{3}$,CH = BC - BH = 7,
∴在Rt△CFH中,CF = $\sqrt{CH^{2}+FH^{2}}=2\sqrt{13}$,
∴PE + PC的最小值为$2\sqrt{13}$。

9. $2\sqrt{13}$ [解析]如图,在AB上取点F,使BF = BE = 2,连接PF,CF,过点F作FH⊥BC于点H。
∵点I是△ABC的内心,
∴BI平分∠ABC,
∴∠ABD = ∠CBD。
又BP = BP,
∴△BFP≌△BEP(SAS),
∴PF = PE,
∴PE + PC = PF + PC≥CF,
∴当C,P,F三点共线时,PE + PC最小,最小值为CF的长。
∵FH⊥BC,∠ABC = 60°,
∴∠BFH = 30°,
∴BH = $\frac{1}{2}BF = 1$,
∴在Rt△BFH中,FH = $\sqrt{BF^{2}-BH^{2}}=\sqrt{3}$,CH = BC - BH = 7,
∴在Rt△CFH中,CF = $\sqrt{CH^{2}+FH^{2}}=2\sqrt{13}$,
∴PE + PC的最小值为$2\sqrt{13}$。

10(中考新考法 分类讨论)若一个直角三角形的两边长分别为3和4,求第三边的长.
答案:
10. 设第三边长为x。当第三边为斜边时,x = $\sqrt{3^{2}+4^{2}}=5$。当第三边为直角边时,x = $\sqrt{4^{2}-3^{2}}=\sqrt{7}$。综上,第三边的长为5或$\sqrt{7}$。
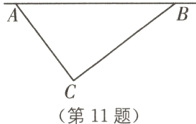
11(新情境 飞机洒水扑灭火灾)森林火灾是一种常见的自然灾害,危害很大,随着中国科技、经济的不断发展,开始应用飞机洒水的方式扑灭火源.如图,有一台救火飞机沿东西方向AB,由点A飞向点B,已知点C为其中一个着火点,且点C与直线AB上两点A,B的距离分别为600 m和800 m,又AB = 1000 m,飞机中心周围500 m以内可以受到洒水影响.
(1)着火点C受洒水影响吗?为什么?
(2)若飞机的速度为10 m/s,要想扑灭着火点C估计需要13 s,请你通过计算判断着火点C能否被扑灭.
(1)着火点C受洒水影响吗?为什么?
(2)若飞机的速度为10 m/s,要想扑灭着火点C估计需要13 s,请你通过计算判断着火点C能否被扑灭.

答案:
11.
(1)着火点C受洒水影响. 理由如下:
如图,过点C作CD⊥AB于点D,
由题意知AC = 600 m,BC = 800 m,AB = 1 000 m,
∵AC² + BC² = 600² + 800² = 1 000²,AB² = 1 000²,
∴AC² + BC² = AB²,
∴△ABC是直角三角形,
∴$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}CD\cdot AB$,
∴600×800 = 1 000 CD,
∴CD = 480 m.
∵飞机中心周围500 m以内可以受到洒水影响,
∴着火点C受洒水影响.

(2)如图,当EC = FC = 500 m时,飞机正好喷到着火点C.
∵CE = CF,CD⊥EF,
∴DE = DF.
在Rt△CDE中,ED² = EC² - CD² = 500² - 480² = 19 600,
∴ED = 140 m,
∴EF = 280 m.
∵飞机的速度为10 m/s,
∴280÷10 = 28(s).
∵28 s>13 s,
∴着火点C能被扑灭.
11.
(1)着火点C受洒水影响. 理由如下:
如图,过点C作CD⊥AB于点D,
由题意知AC = 600 m,BC = 800 m,AB = 1 000 m,
∵AC² + BC² = 600² + 800² = 1 000²,AB² = 1 000²,
∴AC² + BC² = AB²,
∴△ABC是直角三角形,
∴$S_{\triangle ABC}=\frac{1}{2}AC\cdot BC=\frac{1}{2}CD\cdot AB$,
∴600×800 = 1 000 CD,
∴CD = 480 m.
∵飞机中心周围500 m以内可以受到洒水影响,
∴着火点C受洒水影响.

(2)如图,当EC = FC = 500 m时,飞机正好喷到着火点C.
∵CE = CF,CD⊥EF,
∴DE = DF.
在Rt△CDE中,ED² = EC² - CD² = 500² - 480² = 19 600,
∴ED = 140 m,
∴EF = 280 m.
∵飞机的速度为10 m/s,
∴280÷10 = 28(s).
∵28 s>13 s,
∴着火点C能被扑灭.
5.复习题T9·变式 有理数a与b在数轴上的位置如图所示,请用“>”或“<”填空:

①a________0;②b________0;③a________b;
④a - b________0.

①a________0;②b________0;③a________b;
④a - b________0.
答案:
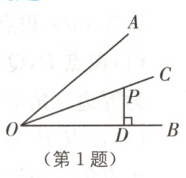
1 教材P31例3·变式(2024·青海中考)如图,OC平分∠AOB,点P在OC上,PD⊥OB,PD = 2,则点P到OA的距离是( ).
A. 4
B. 3
C. 2
D. 1

A. 4
B. 3
C. 2
D. 1
答案:
C
12(中考新考法 数形结合)数与形是数学中的两个最古老,也是最基本的研究对象.数与形也是有联系的,这种联系称为“数形结合”.利用“数形结合”思想可以直观地帮助我们解决一些数学验证或运算.
(1)我国是最早了解勾股定理的国家之一,该定理阐明了直角三角形的三边关系.请你利用如图对勾股定理(即下列命题)进行验证,从中体会“数形结合”的思想:
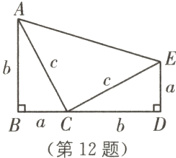
已知:如图,在Rt△ABC和Rt△CDE中,∠B = ∠D = ∠ACE = 90°(点B,C,D在一条直线上),AB = CD = b,BC = DE = a,AC = EC = c.证明:$a^{2}+b^{2}=c^{2}$.
(2)请利用“数形结合”思想,画图推算出$(a + b + c)^{2}$的结果.
(1)我国是最早了解勾股定理的国家之一,该定理阐明了直角三角形的三边关系.请你利用如图对勾股定理(即下列命题)进行验证,从中体会“数形结合”的思想:
已知:如图,在Rt△ABC和Rt△CDE中,∠B = ∠D = ∠ACE = 90°(点B,C,D在一条直线上),AB = CD = b,BC = DE = a,AC = EC = c.证明:$a^{2}+b^{2}=c^{2}$.
(2)请利用“数形结合”思想,画图推算出$(a + b + c)^{2}$的结果.

答案:
12.
(1)梯形ABDE的面积 = $2\times\frac{1}{2}ab+\frac{1}{2}c^{2}$,
梯形ABDE的面积 = $\frac{(a + b)\times(a + b)}{2}$,
∴$2\times\frac{1}{2}ab+\frac{1}{2}c^{2}=\frac{(a + b)\times(a + b)}{2}$,
化简可得$a^{2}+b^{2}=c^{2}$;
(2)如图,
大正方形的面积 = $(a + b + c)^{2}$,
大正方形的面积 = $a^{2}+b^{2}+c^{2}+2ab + 2bc + 2ac$,
∴$(a + b + c)^{2}=a^{2}+b^{2}+c^{2}+2ab + 2bc + 2ac$。

12.
(1)梯形ABDE的面积 = $2\times\frac{1}{2}ab+\frac{1}{2}c^{2}$,
梯形ABDE的面积 = $\frac{(a + b)\times(a + b)}{2}$,
∴$2\times\frac{1}{2}ab+\frac{1}{2}c^{2}=\frac{(a + b)\times(a + b)}{2}$,
化简可得$a^{2}+b^{2}=c^{2}$;
(2)如图,
大正方形的面积 = $(a + b + c)^{2}$,
大正方形的面积 = $a^{2}+b^{2}+c^{2}+2ab + 2bc + 2ac$,
∴$(a + b + c)^{2}=a^{2}+b^{2}+c^{2}+2ab + 2bc + 2ac$。

查看更多完整答案,请扫码查看


