《2025年1课3练江苏人民出版社八年级数学下册北师大版》

1 如图，在等腰直角三角形ABC中，∠BAC = 90°，一把三角尺的直角顶点与BC边的中点O重合，且两条直角边分别经过点A和点B，将三角尺绕点O按顺时针方向旋转任意一个锐角，当三角尺的两直角边与AB，AC分别交于点E，F时，下列结论中，错误的是(　　　)．

A. AE+AF=AC
B. ∠BEO+∠OFC=180°
C. OE+OF=$\frac{\sqrt{2}}{2}$BC
D. $S_{四边形AEOF}=\frac{1}{2}S_{\triangle ABC}$

答案： 1. C

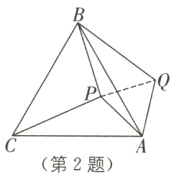
2 如图，P是等边三角形ABC内一点，将线段AP绕点A顺时针旋转60°得到线段AQ，连接BQ，BP，CP. 若PA = 6，PB = 8，PC = 10，求四边形APBQ的面积.

答案：
2. 如图，连接PQ.
由旋转的性质可知AP = AQ，∠PAQ = 60°，
∴△PAQ是等边三角形，
∴PQ = PA = 6，
∴$S_{\triangle PAQ}=\frac{1}{2}\times6\times3\sqrt{3}=9\sqrt{3}$.
∵△ABC是等边三角形，
∴∠CAB = 60°，AC = AB，
∴∠CAB = ∠PAQ = 60°，
∴∠CAB - ∠BAP = ∠PAQ - ∠BAP，即∠CAP = ∠BAQ.
在△ACP和△ABQ中，
$\begin{cases}AC = AB,\\\angle CAP = \angle BAQ,\\AP = AQ,\end{cases}$

∴△ACP≌△ABQ(SAS)，
∴BQ = PC = 10.
∵$PB^{2}+PQ^{2}=8^{2}+6^{2}=100$，
$BQ^{2}=100$，
∴$PB^{2}+PQ^{2}=BQ^{2}$，
∴△BPQ是直角三角形，且∠BPQ = 90°.
∴$S_{\triangle BPQ}=\frac{1}{2}\times6\times8 = 24$，
∴$S_{四边形APBQ}=S_{\triangle BPQ}+S_{\triangle PAQ}=24 + 9\sqrt{3}$.

3 如图，将一块含30°角的直角三角板放置在平行线a，b之间，且较长直角边靠在直线a上，然后将三角板绕着顶点A逆时针旋转25°，使另一个顶点B恰好落在直线b上，这时直角边BC与直线b所构成的∠1等于(　　　)．

A. 55°
B. 60°
C. 65°
D. 70°

答案： 3. C

4 中考新考法 猜想证明 如图(1)，将两张完全相同的三角形纸片ABC和DEC重合放置，其中∠C = 90°，∠B = ∠E = 30°．
(1)如图(2)，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，
①线段DE与AC的位置关系是________；
②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是________．
(2)当△DEC绕点C旋转到如图(3)所示的位置时，小明猜想(1)中S1与S2的数量关系仍然成立，并尝试分别作出了△BDC和△AEC中BC，CE边上的高，请你证明小明的猜想.
　　　　　　　　　　　　　　　　　　　　　　 　
　　　　　　　　　　　　　　　　　　　　　　　　　　

答案： 4.
(1)①DE//AC ②$S_{1}=S_{2}$
(2)由题意，得△ABC≌△DEC，
∴AC = DC，BC = CE.
∵∠DCE = ∠ACB = 90°，
∴∠DCM + ∠ACE = 180°.
又∠ACN + ∠ACE = 180°，
∴∠ACN = ∠DCM.
∵DM⊥BC，AN⊥CN，
∴∠CNA = ∠CMD = 90°.
在△ANC和△DMC中，$\begin{cases}\angle ACN = \angle DCM,\\\angle CNA = \angle CMD,\\AC = DC,\end{cases}$
∴△ANC≌△DMC(AAS)，
∴AN = DM.
又CE = BC，
∴$\frac{1}{2}BC\cdot DM=\frac{1}{2}CE\cdot AN$，即$S_{1}=S_{2}$.