《2025年1课3练江苏人民出版社八年级数学下册北师大版》

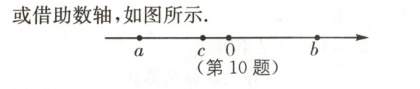
10 （2023·临沂中考）在实数a，b，c中，若a + b = 0，b - c＞c - a＞0，则下列结论：①|a|＞|b|；②a＞0；③b＜0；④c＜0，正确的个数有(　　　)．
A. 1个
B. 2个
C. 3个
D. 4个

答案：
A　[解析]
∵a + b = 0，
∴|a| = |b|，故①错误;
　
∵b - c＞c - a＞0，
∴b＞c＞a. 　又a + b = 0，
∴a<0,b>0，故②③错误;
　
∵a + b = 0，
∴b = - a.
　
∵b - c＞c - a＞0，
∴-a - c＞c - a，
∴-c＞c，
∴c<0,故④正确

11 由m＞n得到(a - 1)m＜(a - 1)n，需要满足的条件是(　　　)．
A. a＞0
B. a＜0
C. a＞1
D. a＜1

答案： D

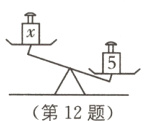
12 跨学科 天平 如图，x和5分别表示天平上两边的砝码的质量，请你用“＞”或“＜”填空：x - 3________2.

答案： <

13 若2a + 3b - 1＞3a + 2b，试比较a，b的大小.

答案： 两边同时减去$2a + 2b$，得$b - 1＞a$， 　两边同时加1，得$b＞a + 1$. 　因为$a + 1＞a$，所以$b＞a$.

14 已知x＞y.
(1)比较9 - x与9 - y的大小，并说明理由；
(2)若mx + 4＜my + 4，求m的取值范围.

答案：
(1)$9 - x<9 - y$. 理由如下： $∵x>y$，$∴-x<-y$(不等式的基本性质3)， $∴9 - x<9 - y$(不等式的基本性质1).
(2)$∵mx + 4y$，即$x - y>0$. 将$m(x - y)<0$两边同时除以$(x - y)$，解得$m<0$

15 （2024·河南周口期末）根据等式和不等式的基本性质，我们可以得到比较两数大小的方法：
若a - b＞0，则a＞b；若a - b = 0，则a = b；若a - b＜0，则a＜b，反之也成立，这种比较大小的方法称为“作差法比较大小”.
(1)若a - b - 6＞0，则a - 3________b + 3（填“＞”“=”或“＜”）；
(2)若$M=\frac{1}{2}(2x^{2}-y^{2}+3)$，$N=\frac{1}{3}(x^{2}-2y^{2}+2)$，试比较M，N的大小，并说明理由.

答案：
(1)＞　[解析]
∵$a - b - 6＞0$，
∴$a - 3 - b - 3＞0$，即$a - 3-(b + 3)＞0$，
∴$a - 3＞b + 3$. 　故答案为＞. 　
(2)$M＞N$.理由如下:
∵$M - N=\frac{1}{2}(2x^{2}-y^{2}+3)-\frac{1}{3}(x^{2}-2y^{2}+2)=\frac{1}{6}(4x^{2}+y^{2}+5)＞0$，
∴$M＞N$.

16 中考新考法 解题方法型阅读理解题 阅读以下材料：
已知两个正整数的和与积相等，求这两个正整数.
解：不妨设这两个正整数为a和b，且a≤b.
由题意，得ab = a + b，(*)
则ab = a + b≤b + b = 2b，所以a≤2.
因为a为正整数，所以a = 1或2.
①当a = 1时，代入等式(*)，得1×b = 1 + b，b不存在；
②当a = 2时，代入等式(*)，得2×b = 2 + b，b = 2，
所以这两个正整数为2和2.
根据阅读材料的启示，思考是否存在三个正整数，它们的和与积相等.试说明你的理由.

答案： 存在三个正整数，它们的和与积相等.理由如下:假设存在三个正整数，它们的和与积相等. 　不妨设这三个正整数为$a$，$b$，$c$，且$a\leqslant b\leqslant c$， 　则$abc = a + b + c$，(*) 　所以$abc = a + b + c\leqslant c + c + c = 3c$，所以$ab\leqslant3$. 　若$a\geqslant2$，则$b\geqslant a\geqslant2$， 　所以$ab\geqslant4$，与$ab\leqslant3$矛盾. 　因此$a = 1$，$b = 1$或2或3. 　①当$a = 1$，$b = 1$时，代入等式(*)，得$1×1×c = 1 + 1 + c$，$c$不存在; 　②当$a = 1$，$b = 2$时，代入等式(*)，得$1×2×c = 1 + 2 + c$，$c = 3$; 　③当$a = 1$，$b = 3$时，代入等式(*)，得$1×3×c = 1 + 3 + c$，$c = 2$，与$b\leqslant c$矛盾，舍去. 　故$a = 1$，$b = 2$，$c = 3$，因此假设成立，即存在三个正整数1，2，3，它们的和与积相等.