2025年1课3练江苏人民出版社八年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1课3练江苏人民出版社八年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第5页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
9 中考新考法 新定义问题 (2024·浙江宁波北仑区期末)定义:若三角形满足其中两边之和等于第三边的三倍,则称该三角形为“三倍三角形”.若等腰三角形ABC是三倍三角形,且其中一边长为3,则△ABC的周长为________.
答案:
12或8 [解析]如果底边长是3,若两腰的和是3的三倍,即为9,满足三角形三边关系定理,则△ABC的周长是9 + 3=12;若腰与底边的和是腰长的三倍,则腰长是1.5,不满足三角形三边关系定理. 如果腰长是3,若两腰的和是底边的三倍,则底边长是2,满足三角形三边关系定理,则△ABC的周长是3 + 3 + 2=8;若腰与底边的和是腰长的三倍,求出底边长是6,不满足三角形三边关系定理.
∴△ABC的周长为12或8.
∴△ABC的周长为12或8.
10 如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;
再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;
再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;….
这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=________.
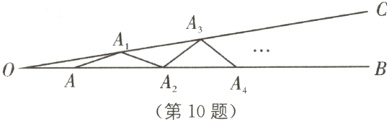
以A为圆心,1为半径向右画弧交OC于点A1,得第1条线段AA1;
再以A1为圆心,1为半径向右画弧交OB于点A2,得第2条线段A1A2;
再以A2为圆心,1为半径向右画弧交OC于点A3,得第3条线段A2A3;….
这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=________.

答案:
9
11 如图,AM//BN,∠BCM和∠CBN的平分线交于点D,DE//BN交BC于点E. (解答过程要求写出每步推导的理由)
(1)求∠BDC的度数;
(2)若AB=AC,求证:AE⊥BC.
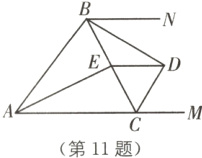
(1)求∠BDC的度数;
(2)若AB=AC,求证:AE⊥BC.

答案:
(1)
∵BN//AM(已知),
∴∠CBN + ∠BCM=180°(两直线平行,同旁内角互补).
∵BD,CD 分别是∠CBN,∠BCM 的平分线(已知),
∴∠NBD=∠DBE=$\frac{1}{2}$∠NBC,∠ECD=∠DCM=$\frac{1}{2}$∠BCM(角平分线的定义),
∴∠DBC + ∠ECD=$\frac{1}{2}$(∠NBC + ∠BCM)=90°(等式的性质),
∴∠BDC=180° - (∠DBC + ∠ECD)=90°(三角形内角和定理).
(2)
∵DE//BN(已知),
∴∠NBD=∠BDE(两直线平行,内错角相等).
∵∠NBD=∠DBE(已证),
∴∠BDE=∠DBE(等量代换),
∴EB=ED(等角对等边).
∵AM//BN(已知),
∴DE//AM(平行于同一条直线的两条直线平行),
∴∠EDC=∠DCM(两直线平行,内错角相等).
∵∠DCM=∠ECD(已证),
∴∠EDC=∠ECD(等量代换),
∴EC=ED(等角对等边),
∴EB=EC(等量代换).
∵AB=AC(已知),
∴AE⊥BC(等腰三角形的三线合一).
(1)
∵BN//AM(已知),
∴∠CBN + ∠BCM=180°(两直线平行,同旁内角互补).
∵BD,CD 分别是∠CBN,∠BCM 的平分线(已知),
∴∠NBD=∠DBE=$\frac{1}{2}$∠NBC,∠ECD=∠DCM=$\frac{1}{2}$∠BCM(角平分线的定义),
∴∠DBC + ∠ECD=$\frac{1}{2}$(∠NBC + ∠BCM)=90°(等式的性质),
∴∠BDC=180° - (∠DBC + ∠ECD)=90°(三角形内角和定理).
(2)
∵DE//BN(已知),
∴∠NBD=∠BDE(两直线平行,内错角相等).
∵∠NBD=∠DBE(已证),
∴∠BDE=∠DBE(等量代换),
∴EB=ED(等角对等边).
∵AM//BN(已知),
∴DE//AM(平行于同一条直线的两条直线平行),
∴∠EDC=∠DCM(两直线平行,内错角相等).
∵∠DCM=∠ECD(已证),
∴∠EDC=∠ECD(等量代换),
∴EC=ED(等角对等边),
∴EB=EC(等量代换).
∵AB=AC(已知),
∴AE⊥BC(等腰三角形的三线合一).
12 中考新考法 归纳一般结论 (1)如图(1),已知:在△ABC中,AB=AC=10,BD平分∠ABC,CD平分∠ACB,过点D作EF//BC,分别交AB,AC于E,F两点,则图中共有________个等腰三角形;EF与BE,CF之间的数量关系是________________,△AEF的周长是________.
(2)如图(2),若将(1)中“在△ABC中,AB=AC=10”改为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有几个等腰三角形?EF与BE,CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长.
(3)已知:如图(3),点D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE//BC,分别交AB,AC于E,F两点,则EF与BE,CF之间又有何数量关系呢?直接写出结论.
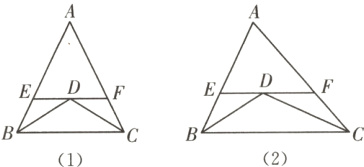
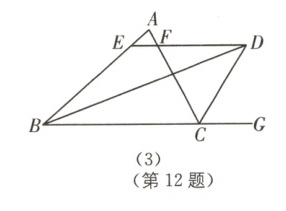
(2)如图(2),若将(1)中“在△ABC中,AB=AC=10”改为“若△ABC为不等边三角形,AB=8,AC=10”其余条件不变,则图中共有几个等腰三角形?EF与BE,CF之间的数量关系是什么?证明你的结论,并求出△AEF的周长.
(3)已知:如图(3),点D在△ABC外,AB>AC,且BD平分∠ABC,CD平分△ABC的外角∠ACG,过点D作DE//BC,分别交AB,AC于E,F两点,则EF与BE,CF之间又有何数量关系呢?直接写出结论.


答案:
(1)5 BE + CF=EF 20
(2)图中有2个等腰三角形,BE + CF=EF,△AEF的周长为18. 证明如下:
∵BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠CBD,∠FCD=∠BCD.
∵EF//BC,
∴∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EBD=∠EDB,∠FDC=∠FCD,
∴BE=DE,CF=DF,
∴等腰三角形有△BDE,△CFD,BE + CF=DE + DF=EF,即BE + CF=EF.可得△AEF的周长为18.
(3)BE - CF=EF.
(1)5 BE + CF=EF 20
(2)图中有2个等腰三角形,BE + CF=EF,△AEF的周长为18. 证明如下:
∵BD平分∠ABC,CD平分∠ACB,
∴∠EBD=∠CBD,∠FCD=∠BCD.
∵EF//BC,
∴∠EDB=∠CBD,∠FDC=∠BCD,
∴∠EBD=∠EDB,∠FDC=∠FCD,
∴BE=DE,CF=DF,
∴等腰三角形有△BDE,△CFD,BE + CF=DE + DF=EF,即BE + CF=EF.可得△AEF的周长为18.
(3)BE - CF=EF.
查看更多完整答案,请扫码查看


