2025年1课3练江苏人民出版社八年级数学下册北师大版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1课3练江苏人民出版社八年级数学下册北师大版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第20页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
14 若三角形三边长分别为a²+b²,2ab,a²-b²,则这个三角形是( ).
A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 不能确定
A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 不能确定
答案:
B
15 已知在等腰三角形ABC中,AB = AC,D为边BC所在直线上一点,连接AD,若△ACD和△ABD都是等腰三角形,则∠C的度数是__________.
答案:
36°或45°或72°
16 如图,已知点B,F,C,E在同一直线上,AB⊥BE,垂足为B,DE⊥BE,垂足为E,且AB = DE. 请你添加一个条件,使AC = DF(不再添加其他线段,不再标注或使用其他字母),并给出证明.
添加的条件是:__________.
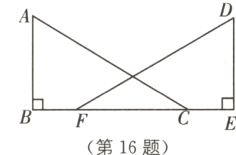
添加的条件是:__________.

答案:
添加的条件:BC = EF(或∠A = ∠D或∠ACB = ∠DFE或BF = CE等).
证明如下(以添加条件BC = EF为例):
∵AB⊥BE,DE⊥BE,
∴∠ABC = ∠DEF = 90°.
∵BC = EF,AB = DE,
∴△ABC≌△DEF(SAS),
∴AC = DF.
证明如下(以添加条件BC = EF为例):
∵AB⊥BE,DE⊥BE,
∴∠ABC = ∠DEF = 90°.
∵BC = EF,AB = DE,
∴△ABC≌△DEF(SAS),
∴AC = DF.
17 中考新考法 归纳一般结论 某数学兴趣小组开展了一次活动,过程如下:
设∠BAC =θ(0°<θ<90°),现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC 上.
活动一:如图(1)所示,从点A₁;开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,A₁A₂为第1根小棒.
思考:(1)小棒能无限摆下去吗?答: (填“能”或“不能”) (2)设AA₁=A₁A₂=A₂A₃=1
①θ=
若记小棒 的长度为an(n为正整数),如A₁A₂=a1,A₃A₄=a₂, …,求出此时a₂a₃的值,并直接写出aₙ
的长度为an(n为正整数),如A₁A₂=a1,A₃A₄=a₂, …,求出此时a₂a₃的值,并直接写出aₙ
(用含n的式子表示)
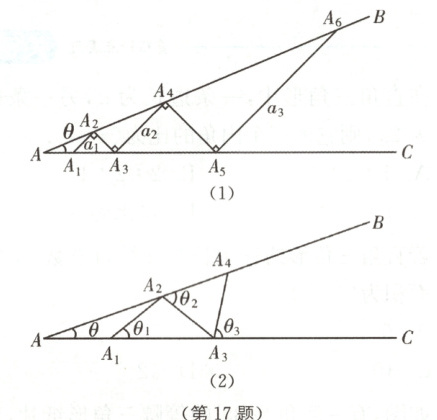
活动二:
如图(2)所示,从点A₁开始,用等长的小棒依次向右摆放,其中A₁A₂为第1根小棒,且A₁A₂=AA₁
设∠BAC =θ(0°<θ<90°),现把小棒依次摆放在两射线之间,并使小棒两端分别落在射线AB,AC 上.
活动一:如图(1)所示,从点A₁;开始,依次向右摆放小棒,使小棒与小棒在端点处互相垂直,A₁A₂为第1根小棒.
思考:(1)小棒能无限摆下去吗?答: (填“能”或“不能”) (2)设AA₁=A₁A₂=A₂A₃=1
①θ=
若记小棒
 的长度为an(n为正整数),如A₁A₂=a1,A₃A₄=a₂, …,求出此时a₂a₃的值,并直接写出aₙ
的长度为an(n为正整数),如A₁A₂=a1,A₃A₄=a₂, …,求出此时a₂a₃的值,并直接写出aₙ(用含n的式子表示)

活动二:
如图(2)所示,从点A₁开始,用等长的小棒依次向右摆放,其中A₁A₂为第1根小棒,且A₁A₂=AA₁
数学思考:
(3)若已经摆放了3根小棒,
θ1= θ2= θ3= ,(用含θ的式子表示)
答案:
(1)能
(2)①22.5°
②
∵AA₁ = A₁A₂ = A₂A₃ = 1,A₁A₂⊥A₂A₃,
∴A₁A₃ = $\sqrt{2}$,AA₃ = 1 + $\sqrt{2}$.
又A₂A₃⊥A₃A₄,
∴A₁A₂//A₃A₄.
同理A₃A₄//A₅A₆.
∴∠A = ∠AA₂A₁ = ∠AA₄A₃ = ∠AA₆A₅.
∴AA₃ = A₃A₄,AA₅ = A₅A₆.
∴a₂ = A₃A₄ = AA₃ = 1 + $\sqrt{2}$,a₃ = AA₃ + A₃A₅ = a₂ + A₃A₅.
∵A₃A₅ = $\sqrt{2}a₂$,
∴a₃ = A₅A₆ = AA₅ = a₂ + $\sqrt{2}a₂ = (\sqrt{2} + 1)^2$.
∴aₙ = ($\sqrt{2} + 1)^{n - 1}$.
(3)2θ 3θ 4θ
(1)能
(2)①22.5°
②
∵AA₁ = A₁A₂ = A₂A₃ = 1,A₁A₂⊥A₂A₃,
∴A₁A₃ = $\sqrt{2}$,AA₃ = 1 + $\sqrt{2}$.
又A₂A₃⊥A₃A₄,
∴A₁A₂//A₃A₄.
同理A₃A₄//A₅A₆.
∴∠A = ∠AA₂A₁ = ∠AA₄A₃ = ∠AA₆A₅.
∴AA₃ = A₃A₄,AA₅ = A₅A₆.
∴a₂ = A₃A₄ = AA₃ = 1 + $\sqrt{2}$,a₃ = AA₃ + A₃A₅ = a₂ + A₃A₅.
∵A₃A₅ = $\sqrt{2}a₂$,
∴a₃ = A₅A₆ = AA₅ = a₂ + $\sqrt{2}a₂ = (\sqrt{2} + 1)^2$.
∴aₙ = ($\sqrt{2} + 1)^{n - 1}$.
(3)2θ 3θ 4θ
查看更多完整答案,请扫码查看


