《2025年1课3练江苏人民出版社八年级数学下册北师大版》

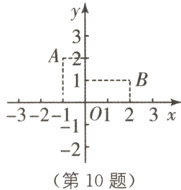
10 如图，在平面直角坐标系中有O，A，B三点，现需要在平面内找一点C，使以点O，A，B，C为顶点的四边形是平行四边形，则点C的坐标不可能为( )．
A. (-1,3)
B. (1,3)
C. (3,-1)
D. (-3,1)
　　　

答案： 答案：A
解析：本题可分三种情况讨论以点$O$，$A$，$B$，$C$为顶点的四边形是平行四边形时，点$C$的坐标。
设$O(0,0)$，$A(2,1)$，$B(1, - 2)$。
- **当$OB$为平行四边形的对角线时**
根据平行四边形的对角线互相平分，可得$OB$的中点坐标为$(\frac{0 + 1}{2}, \frac{0 - 2}{2}) = (\frac{1}{2}, - 1)$。
因为$AC$的中点与$OB$的中点重合，设$C(x,y)$，则$\frac{2 + x}{2} = \frac{1}{2}$，$\frac{1 + y}{2} = - 1$，
解得$x = - 1$，$y = - 3$，此时$C$点坐标为$( - 1, - 3)$。
- **当$OA$为平行四边形的对角线时**
$OA$的中点坐标为$(\frac{0 + 2}{2}, \frac{0 + 1}{2}) = (1, \frac{1}{2})$。
因为$BC$的中点与$OA$的中点重合，设$C(x,y)$，则$\frac{1 + x}{2} = 1$，$\frac{ - 2 + y}{2} = \frac{1}{2}$，
解得$x = 1$，$y = 3$，此时$C$点坐标为$(1,3)$。
- **当$AB$为平行四边形的对角线时**
$AB$的中点坐标为$(\frac{2 + 1}{2}, \frac{1 - 2}{2}) = (\frac{3}{2}, - \frac{1}{2})$。
因为$OC$的中点与$AB$的中点重合，设$C(x,y)$，则$\frac{0 + x}{2} = \frac{3}{2}$，$\frac{0 + y}{2} = - \frac{1}{2}$，
解得$x = 3$，$y = - 1$，此时$C$点坐标为$(3, - 1)$。
综上，点$C$的坐标不可能为$( - 1,3)$，答案选A。

11 如图，BD平分∠ABC，∠1=∠2，AD=BC=5，则CD=__________.
　　

答案： 答案：5
解析：本题可先根据角平分线的性质和平行线的判定定理证明$AD// BC$，再根据平行四边形的判定定理证明四边形$ABCD$是平行四边形，最后根据平行四边形的性质求出$CD$的长。
- **证明$AD// BC$**
因为$BD$平分$\angle ABC$，所以$\angle ABD = \angle DBC$。
又因为$\angle 1 = \angle 2$，所以$\angle 2 = \angle DBC$，根据内错角相等，两直线平行，可得$AD// BC$。
- **证明四边形$ABCD$是平行四边形**
因为$AD// BC$，$AD = BC$，根据一组对边平行且相等的四边形是平行四边形，可知四边形$ABCD$是平行四边形。
- **求$CD$的长**
因为四边形$ABCD$是平行四边形，根据平行四边形的对边相等，可得$CD = AD = 5$。
综上，答案为$5$。

12 如图，点A，B，C，D在网格中小正方形的顶点处，AD与BC相交于点O，若小正方形的边长为1，则DO的长为__________.
　　　

答案： 答案：3
解析：本题可通过构造相似三角形，利用相似三角形的性质来求出$DO$的长。
过点$D$作$DE// BC$交$AB$的延长线于点$E$。
因为$DE// BC$，所以$\triangle AOD\sim\triangle AED$，$\triangle ABC\sim\triangle AED$。
由网格可知$BC = \sqrt{2^{2} + 1^{2}} = \sqrt{5}$，$DE = \sqrt{4^{2} + 2^{2}} = 2\sqrt{5}$。
因为$\triangle ABC\sim\triangle AED$，所以$\frac{BC}{DE} = \frac{AB}{AE} = \frac{1}{2}$，则$AE = 2AB$。
又因为$\triangle AOD\sim\triangle AED$，所以$\frac{DO}{DE} = \frac{AO}{AE} = \frac{1}{2}$，即$\frac{DO}{2\sqrt{5}} = \frac{1}{2}$，解得$DO = \sqrt{5}$。
在$Rt\triangle DOB$中，$DB = \sqrt{3^{2} + 1^{2}} = \sqrt{10}$，$OB = \sqrt{2^{2} + 1^{2}} = \sqrt{5}$，根据勾股定理可得$DO = \sqrt{DB^{2} - OB^{2}} = \sqrt{(\sqrt{10})^{2} - (\sqrt{5})^{2}} = \sqrt{10 - 5} = \sqrt{5} = 3$。
综上，答案为$3$。

13 中考新考法 满足结论的条件开放 (2024·湖南中考)如图，在四边形ABCD中，AB//CD，点E在边AB上，________. 请从“①∠B =∠AED；②AE=BE，AE=CD”这两组条件中任选一组作为已知条件，填在横线上(填序号)，再解决下列问题：
(1)求证：四边形BCDE为平行四边形；
(2)若AD⊥AB，AD=8，BC=10，求线段AE的长.
　　　　　　　　　　　　　

答案： 答案：
(1)选择①，
∵∠B = ∠AED，
∴DE//CB.
∵AB//CD，
∴四边形BCDE为平行四边形；
选择②，
∵AE = BE，AE = CD，
∴CD = BE.
∵AB//CD，
∴四边形BCDE为平行四边形.
(2)由
(1)，得四边形BCDE为平行四边形，
∴DE = BC = 10.
∵AD⊥AB，AD = 8，
∴AE=$\sqrt{DE^{2}-AD^{2}}$= 6.
解析：本题可根据所给条件，结合平行四边形的判定定理证明四边形$BCDE$为平行四边形，再利用勾股定理求出线段$AE$的长。
- **（1）证明四边形$BCDE$为平行四边形**\n**选择条件①**：
因为$\angle B = \angle AED$，根据同位角相等，两直线平行，可得$DE// CB$。
又因为$AB// CD$，根据两组对边分别平行的四边形是平行四边形，可知四边形$BCDE$为平行四边形。\n**选择条件②**：
因为$AE = BE$，$AE = CD$，所以$CD = BE$。
又因为$AB// CD$，根据一组对边平行且相等的四边形是平行四边形，可知四边形$BCDE$为平行四边形。
- **（2）求线段$AE$的长**
由（1）可知四边形$BCDE$为平行四边形，根据平行四边形的对边相等，可得$DE = BC = 10$。
因为$AD\perp AB$，所以$\triangle ADE$是直角三角形。
在$Rt\triangle ADE$中，$AD = 8$，$DE = 10$，根据勾股定理$AE = \sqrt{DE^{2} - AD^{2}} = \sqrt{10^{2} - 8^{2}} = \sqrt{100 - 64} = \sqrt{36} = 6$。
综上，答案依次为（1）选择①，证明过程见上述；选择②，证明过程见上述；（2）$6$。

14 中考新考法 动点问题 如图，在四边形ABCD中，AD//BC，AD=10 cm，BC=15 cm，点P从点A向点D以1 cm/s的速度运动，点Q从点C出发以3 cm/s的速度在CB间往返运动，两个点同时出发，当点P到达点D时停止(同时点Q也停止)．
(1)设当P，Q两点同时出发t秒后，CQ的长为s，请写出s与t之间的函数关系式.
(2)线段PQ将四边形ABCD截成两个四边形，分别为四边形ABQP和四边形PQCD，t为何值时所截得的两个四边形中，其中一个四边形为平行四边形？
　　　　　　　　　　　

答案： 答案：
(1)
∵点P从点A向点D以1 cm/s的速度运动，
∴点P到达点D的时间为$\frac{10}{1}$= 10(s)，
∴当0≤t＜5时，CQ = s = 3t；
当5≤t≤10时，CQ = s = 15 - (3t - 15)= 30 - 3t.
(2)当0≤t＜5时，若四边形PQCD是平行四边形，则PD = CQ，
∴10 - t = 3t，
∴t=$\frac{5}{2}$；
若四边形ABQP是平行四边形，则AP = BQ，
∴t = 15 - 3t，
∴t=$\frac{15}{4}$；
当5≤t≤10时，若四边形PQCD是平行四边形，则PD = CQ，
∴10 - t = 30 - 3t，
∴t = 10(舍去)；
若四边形ABQP是平行四边形，则AP = BQ，
∴t = 3t - 15，
∴t=$\frac{15}{2}$.
综上所述，t的值为$\frac{5}{2}$或$\frac{15}{4}$或$\frac{15}{2}$.
解析：本题可根据点$P$和点$Q$的运动速度和方向，分情况讨论$CQ$的长与时间$t$的函数关系式，再根据平行四边形的性质求出$t$的值。
- **（1）求$s$与$t$之间的函数关系式**
已知点$P$从点$A$向点$D$以$1cm/s$的速度运动，$AD = 10cm$，则点$P$到达点$D$的时间为$\frac{10}{1} = 10s$。\n当$0\leq t\lt 5$时，点$Q$从点$C$向点$B$运动，$CQ$的长为$s = 3t$。\n当$5\leq t\leq 10$时，点$Q$从点$B$向点$C$运动，此时$CQ$的长为$s = 15 - (3t - 15) = 30 - 3t$。\n**（2）求$t$的值**\n当$0\leq t\lt 5$时：
若四边形$PQCD$是平行四边形，则$PD = CQ$，因为$PD = 10 - t$，$CQ = 3t$，所以$10 - t = 3t$，
移项可得$3t + t = 10$，
即$4t = 10$，
解得$t = \frac{5}{2}$。
若四边形$ABQP$是平行四边形，则$AP = BQ$，因为$AP = t$，$BQ = 15 - 3t$，所以$t = 15 - 3t$，
移项可得$3t + t = 15$，
即$4t = 15$，
解得$t = \frac{15}{4}$。\n当$5\leq t\leq 10$时：
若四边形$PQCD$是平行四边形，则$PD = CQ$，因为$PD = 10 - t$，$CQ = 30 - 3t$，所以$10 - t = 30 - 3t$，
移项可得$3t - t = 30 - 10$，
即$2t = 20$，
解得$t = 10$，此时点$P$到达点$D$，不符合题意，舍去。
若四边形$ABQP$是平行四边形，则$AP = BQ$，因为$AP = t$，$BQ = 3t - 15$，所以$t = 3t - 15$，
移项可得$3t - t = 15$，
即$2t = 15$，
解得$t = \frac{15}{2}$。
综上，$t$的值为$\frac{5}{2}$或$\frac{15}{4}$或$\frac{15}{2}$。