《2025年1课3练江苏人民出版社八年级数学下册北师大版》

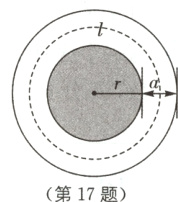
17 如图，在半径为$r$的圆形土地周围有一条宽为$a$的路，这条路的面积用$S$表示，通过这条道路正中的圆周长用$l$表示。
(1)写出用$a,r$表示$S$的代数式；
(2)找出$l$与$S$之间的关系式。

答案：
(1)$S=\pi(r + a)^{2}-\pi r^{2}=\pi(r + a + r)(r + a - r)=\pi a(2r + a)$.
(2)$l = 2\pi(r+\frac{a}{2})=\pi(2r + a)$,
则$2r + a=\frac{l}{\pi}$,
$\therefore S=\pi a(2r + a)=\pi a\cdot\frac{l}{\pi}=al$.

18 现有三个多项式：$\frac{1}{2}a^{2}+a - 4,\frac{1}{2}a^{2}+5a + 4,\frac{1}{2}a^{2}-a$。请你选择其中两个进行加法运算，并把结果因式分解。

答案： 当选取$\frac{1}{2}a^{2}+a - 4$与$\frac{1}{2}a^{2}+5a + 4$时,
$(\frac{1}{2}a^{2}+a - 4)+(\frac{1}{2}a^{2}+5a + 4)=a^{2}+6a=a(a + 6)$.
当选取$\frac{1}{2}a^{2}+a - 4$与$\frac{1}{2}a^{2}-a$时,
$(\frac{1}{2}a^{2}+a - 4)+(\frac{1}{2}a^{2}-a)=a^{2}-4=(a + 2)(a - 2)$.
当选取$\frac{1}{2}a^{2}+5a + 4$与$\frac{1}{2}a^{2}-a$时,
$(\frac{1}{2}a^{2}+5a + 4)+(\frac{1}{2}a^{2}-a)=a^{2}+4a + 4=(a + 2)^{2}$. (写出一个即可)

19 中考新考法 操作探究 (2024·四川成都四十三中月考)从边长为$a$的正方形剪掉一个边长为$b$的正方形(如图1)，然后将剩余部分拼成一个长方形(如图2)。

(1)上述操作能验证的等式是______；
(2)若$x^{2}-9y^{2}=12,x + 3y = 4$，求$x - 3y$的值；
(3)计算：$(1-\frac{1}{2^{2}})\times(1-\frac{1}{3^{2}})\times(1-\frac{1}{4^{2}})\times\cdots\times(1-\frac{1}{2022^{2}})\times(1-\frac{1}{2023^{2}})$。

答案：
(1)$a^{2}-b^{2}=(a + b)(a - b)$.
(2)$\because x^{2}-9y^{2}=12$,即$(x + 3y)(x - 3y)=12$,而$x + 3y = 4$,$\therefore x - 3y=12\div4 = 3$.
(3)原式$=(1-\frac{1}{2})\times(1+\frac{1}{2})\times(1-\frac{1}{3})\times(1+\frac{1}{3})\times(1-\frac{1}{4})\times(1+\frac{1}{4})\times\cdots\times(1-\frac{1}{2022})\times(1+\frac{1}{2022})\times(1-\frac{1}{2023})\times(1+\frac{1}{2023})$
$=\frac{1}{2}\times\frac{3}{2}\times\frac{2}{3}\times\frac{4}{3}\times\frac{3}{4}\times\frac{5}{4}\times\cdots\times\frac{2021}{2022}\times\frac{2023}{2022}\times\frac{2022}{2023}\times\frac{2024}{2023}=\frac{1}{2}\times\frac{2024}{2023}=\frac{2024}{4046}=\frac{1012}{2023}$.

20 中考新考法 解题方法型阅读理解题 阅读材料，回答下列问题：
我们知道对于二次三项式$x^{2}+2ax + a^{2}$这样的完全平方公式，可以用公式将它分解成$(x + a)^{2}$的形式，但是，对于二次三项式$x^{2}+2ax - 3a^{2}$就不能直接用完全平方公式，可以采用如下方法：$x^{2}+2ax - 3a^{2}=x^{2}+2ax + a^{2}-a^{2}-3a^{2}=(x + a)^{2}-(2a)^{2}=(x + 3a)\cdot(x - a)$。
(1)像上面这样把二次三项式分解因式的数学方法是______；
(2)这种方法的关键是______；
(3)用上述方法把$a^{2}-8a + 15$分解因式。

答案：
(1)配方法
(2)凑成完全平方式
(3)$a^{2}-8a + 15=a^{2}-8a + 16-16 + 15=a^{2}-8a + 16-1=(a - 4)^{2}-1=(a - 3)(a - 5)$.