《2025年1课3练江苏人民出版社八年级数学下册北师大版》

8 (2025·河北唐山路南区友谊中学月考)如图，在△AOB和△COD中，OA = OB，OC = OD，OA＜OC，∠AOB = ∠COD = 36°. 连接AC，BD交于点M，连接OM. 下列结论：①∠AMB = 36°，②AC = BD，③OM平分∠AOD，④MO平分∠AMD. 其中正确的结论有(　　　).
　　　
A. 4个　　
　B. 3个　
　C. 2个　
　D. 1个

答案： B　[解析]
∵∠AOB = ∠COD = 36°,
∴∠AOB + ∠BOC = ∠COD + ∠BOC,即∠AOC = ∠BOD.在△AOC和△BOD中，$\begin{cases}OA = OB,\\\angle AOC=\angle BOD,\\OC = OD,\end{cases}$
∴△AOC≌△BOD(SAS),
∴∠OCA = ∠ODB,∠OAC = ∠OBD,AC = BD,②正确;由三角形的外角性质，得∠AMB + ∠OBD = ∠AOB + ∠OAC,
∴∠AMB = ∠AOB = 36°,①正确;如图，过点O作OG⊥AC于点G,OH⊥BD于点H,则∠OGC = ∠OHD = 90°.在△OCG和△ODH中，$\begin{cases}\angle OGC=\angle OHD,\\\angle OCA=\angle ODB,\\OC = OD,\end{cases}$
∴△OCG≌△ODH(AAS),
∴OG = OH,
∴MO平分∠AMD,④正确;假设OM平分∠AOD,则∠BOM = ∠COM.
∵MO平分∠AMD,
∴∠DMO = ∠AMO,
∴∠CMO = ∠BMO.在△COM和△BOM中，$\begin{cases}\angle COM=\angle BOM,\\OM = OM,\\\angle CMO=\angle BMO,\end{cases}$
∴△COM≌△BOM(ASA),
∴OB = OC.
∵OA = OB,
∴OA = OC,与OA＜OC矛盾，
∴③错误.
∴正确的有①②④.故选B.

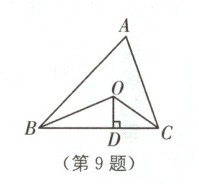
9 如图，已知△ABC的周长是21，OB，OC分别平分∠ABC和∠ACB，OD⊥BC于点D，且OD = 4，△ABC的面积是________.

答案： 42

10 (2025·湖北武汉期中)如图，为了促进当地旅游发展，某地区要修建一个度假村. 要使这个度假村到三条公路的距离相等，这个度假村的选址有________处可供选择.
　　　　　　　　　　　　　　　

答案： 4

11 如图，AD是∠BAC的平分线，DE⊥AB，垂足为E，DF⊥AC，垂足为F，且DB = DC，请你探究BE与CF存在怎样的数量关系? 并说明理由.
　　　　　　　　　　　　

答案： BE = CF.理由如下:
∵AD平分∠BAC,DE⊥AE,DF⊥AC,
∴DE = DF.在Rt△DEB和Rt△DFC中，$\begin{cases}BD = CD,\\DE = DF,\end{cases}$
∴Rt△DEB≌Rt△DFC,
∴BE = CF.

12 如图，已知点P是∠AOB的平分线上的一点，∠AOB = 60°，PD⊥OA，M是OP的中点，DM = 4 cm，如果点C是OB上一个动点，求PC的最小值.
　　　　　　　　　　　　　　

答案：
∵P是∠AOB的平分线上的一点，∠AOB = 60°,
∴∠AOP=$\frac{1}{2}$∠AOB = 30°.
∵PD⊥OA,M是OP的中点,DM = 4cm,∠OPD = 60°,DM = PM,
∴△PDM为等边三角形,
∴PD = DM = 4cm.
∵点C是OB上一个动点,
∴PC的最小值为P到OB的距离,
∴PC的最小值 = PD = 4cm.

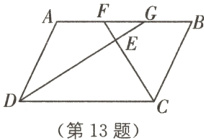
13 中考新考法 满足结论的条件开放 如图，四边形ABCD是平行四边形，∠BCD的平分线CF交AB于点F，∠ADC的平分线DG交AB于点G，DG，CF相交于点E.
(1)求证：AF = GB；
(2)请你在已知条件的基础上再添加一个条件，使得△EFG为等腰直角三角形，请说明理由.
　　　　　　　　　　　　

答案：
(1)
∵四边形ABCD是平行四边形,
∴AB//DC,
∴∠AGD = ∠CDG.
∵DG平分∠ADC,
∴∠ADG = ∠CDG,
∴∠ADG = ∠AGD,
∴AD = AG.同理可证BF = BC.
∵AD = BC,
∴AG = BF,
∴AF = BG.
(2)添加∠A = 90°(答案不唯一).理由如下:由
(1)知∠ADG = ∠AGD = ∠GDC = 45°,同理可得∠BFC = 45°,故△EFG为等腰直角三角形.