2025年同步实践评价课程基础训练高中数学必修第二册
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年同步实践评价课程基础训练高中数学必修第二册 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第7页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
- 第117页
- 第118页
- 第119页
- 第120页
- 第121页
- 第122页
- 第123页
- 第124页
- 第125页
- 第126页
- 第127页
- 第128页
- 第129页
- 第130页
- 第131页
- 第132页
- 第133页
- 第134页
- 第135页
- 第136页
类型2 向量加法运算律的应用
【例2】(1)化简:
①$\overrightarrow{BC}+\overrightarrow{AB}$;
②$\overrightarrow{DB}+\overrightarrow{CD}+\overrightarrow{BC}$;
③$\overrightarrow{AB}+\overrightarrow{DF}+\overrightarrow{CD}+\overrightarrow{BC}+\overrightarrow{FA}$.
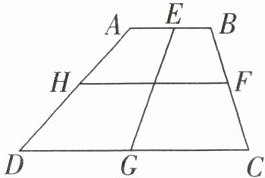
(2)如图,E,F,G,H分别是梯形ABCD的边AB,BC,CD,DA的中点,化简下列各式:
①$\overrightarrow{DG}+\overrightarrow{EA}+\overrightarrow{CB}$;
②$\overrightarrow{EG}+\overrightarrow{CG}+\overrightarrow{DA}+\overrightarrow{EB}$.
【例2】(1)化简:
①$\overrightarrow{BC}+\overrightarrow{AB}$;
②$\overrightarrow{DB}+\overrightarrow{CD}+\overrightarrow{BC}$;
③$\overrightarrow{AB}+\overrightarrow{DF}+\overrightarrow{CD}+\overrightarrow{BC}+\overrightarrow{FA}$.
(2)如图,E,F,G,H分别是梯形ABCD的边AB,BC,CD,DA的中点,化简下列各式:
①$\overrightarrow{DG}+\overrightarrow{EA}+\overrightarrow{CB}$;
②$\overrightarrow{EG}+\overrightarrow{CG}+\overrightarrow{DA}+\overrightarrow{EB}$.

答案:
解:
(1)①$\overrightarrow{BC}+\overrightarrow{AB}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.
②$\overrightarrow{DB}+\overrightarrow{CD}+\overrightarrow{BC}=\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DB}=0$.
③$\overrightarrow{AB}+\overrightarrow{DF}+\overrightarrow{CD}+\overrightarrow{BC}+\overrightarrow{FA}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DF}+\overrightarrow{FA}=0$.
(2)①$\overrightarrow{DG}+\overrightarrow{EA}+\overrightarrow{CB}=\overrightarrow{GC}+\overrightarrow{BE}+\overrightarrow{CB}=\overrightarrow{GC}+\overrightarrow{CB}+\overrightarrow{BE}=\overrightarrow{GB}+\overrightarrow{BE}=\overrightarrow{GE}$.
②$\overrightarrow{EG}+\overrightarrow{CG}+\overrightarrow{DA}+\overrightarrow{EB}=\overrightarrow{EG}+\overrightarrow{GD}+\overrightarrow{DA}+\overrightarrow{AE}=\overrightarrow{ED}+\overrightarrow{DA}+\overrightarrow{AE}=\overrightarrow{EA}+\overrightarrow{AE}=0$.
(1)①$\overrightarrow{BC}+\overrightarrow{AB}=\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$.
②$\overrightarrow{DB}+\overrightarrow{CD}+\overrightarrow{BC}=\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DB}=0$.
③$\overrightarrow{AB}+\overrightarrow{DF}+\overrightarrow{CD}+\overrightarrow{BC}+\overrightarrow{FA}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CD}+\overrightarrow{DF}+\overrightarrow{FA}=0$.
(2)①$\overrightarrow{DG}+\overrightarrow{EA}+\overrightarrow{CB}=\overrightarrow{GC}+\overrightarrow{BE}+\overrightarrow{CB}=\overrightarrow{GC}+\overrightarrow{CB}+\overrightarrow{BE}=\overrightarrow{GB}+\overrightarrow{BE}=\overrightarrow{GE}$.
②$\overrightarrow{EG}+\overrightarrow{CG}+\overrightarrow{DA}+\overrightarrow{EB}=\overrightarrow{EG}+\overrightarrow{GD}+\overrightarrow{DA}+\overrightarrow{AE}=\overrightarrow{ED}+\overrightarrow{DA}+\overrightarrow{AE}=\overrightarrow{EA}+\overrightarrow{AE}=0$.
类型3 向量加法的实际应用
【例3】如图,用两根绳子把重10 N的物体W吊在水平杆子AB上,∠ACW = 150°,∠BCW = 120°,求A和B处所受力的大小(绳子的质量忽略不计).
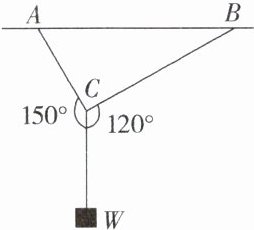
【例3】如图,用两根绳子把重10 N的物体W吊在水平杆子AB上,∠ACW = 150°,∠BCW = 120°,求A和B处所受力的大小(绳子的质量忽略不计).

答案:
解:如图所示,设$\overrightarrow{CE}$,$\overrightarrow{CF}$分别表示A,B所受的力,10 N的重力用$\overrightarrow{CG}$表示,则$\overrightarrow{CE}+\overrightarrow{CF}=\overrightarrow{CG}$.

易得$\angle ECG = 180^{\circ}-150^{\circ}=30^{\circ}$,
$\angle FCG = 180^{\circ}-120^{\circ}=60^{\circ}$.
$\therefore|\overrightarrow{CE}|=|\overrightarrow{CG}|\cdot\cos30^{\circ}=10\times\frac{\sqrt{3}}{2}=5\sqrt{3}$(N),
$|\overrightarrow{CF}|=|\overrightarrow{CG}|\cdot\cos60^{\circ}=10\times\frac{1}{2}=5$(N).
$\therefore$A处所受的力的大小为$5\sqrt{3}$ N,B处所受的力的大小为5 (N).
解:如图所示,设$\overrightarrow{CE}$,$\overrightarrow{CF}$分别表示A,B所受的力,10 N的重力用$\overrightarrow{CG}$表示,则$\overrightarrow{CE}+\overrightarrow{CF}=\overrightarrow{CG}$.

易得$\angle ECG = 180^{\circ}-150^{\circ}=30^{\circ}$,
$\angle FCG = 180^{\circ}-120^{\circ}=60^{\circ}$.
$\therefore|\overrightarrow{CE}|=|\overrightarrow{CG}|\cdot\cos30^{\circ}=10\times\frac{\sqrt{3}}{2}=5\sqrt{3}$(N),
$|\overrightarrow{CF}|=|\overrightarrow{CG}|\cdot\cos60^{\circ}=10\times\frac{1}{2}=5$(N).
$\therefore$A处所受的力的大小为$5\sqrt{3}$ N,B处所受的力的大小为5 (N).
发现规律
利用向量的加法解决实际应用问题的步骤是什么?你认为有哪些关键点和技巧?
(1)利用向量的加法解决实际应用题的三个步骤
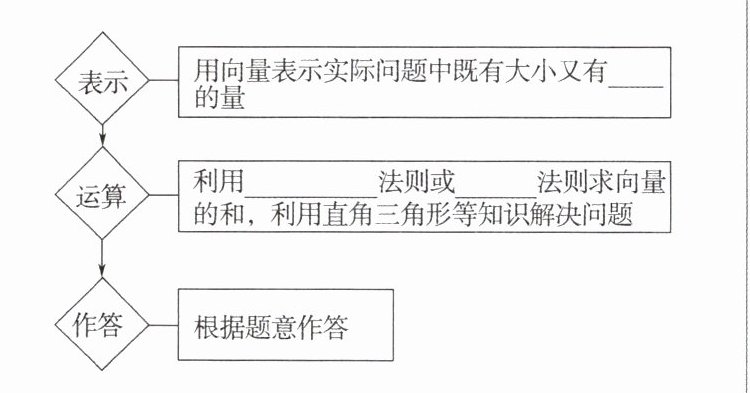
(2)三个关键:一是从向量的角度认识平面图形中各线段之间的关系;二是熟练找出图形中的相等向量和平行向量;三是能根据三角形法则或平行四边形法则作出向量的和向量.
(3)应用技巧:①准确画出几何图形,将几何图形中的边转化为向量;②将所求问题转化为向量的加法运算,进而利用向量加法的几何意义进行求解.
利用向量的加法解决实际应用问题的步骤是什么?你认为有哪些关键点和技巧?
(1)利用向量的加法解决实际应用题的三个步骤

(2)三个关键:一是从向量的角度认识平面图形中各线段之间的关系;二是熟练找出图形中的相等向量和平行向量;三是能根据三角形法则或平行四边形法则作出向量的和向量.
(3)应用技巧:①准确画出几何图形,将几何图形中的边转化为向量;②将所求问题转化为向量的加法运算,进而利用向量加法的几何意义进行求解.
答案:
(1)方向 平行四边形 三角形
(1)方向 平行四边形 三角形
查看更多完整答案,请扫码查看


