《2025年5年中考3年模拟八年级数学下册湘教版》

1.(2024北京海淀期中)下列函数中,是一次函数的是 ( )
A.$y = -\frac{2}{x}$
B.$y = x^{2} - 1$
C.$y = \sqrt{x}$
D.$y = 2x - 1$

答案： D：由一次函数的定义可知，$y = 2x - 1$是一次函数，故选D。

2.[新独家原创]一次函数$y = -3x + b$的图象经过点$(1,3)$,则它的图象与x轴的交点坐标为 ( )
(M8204003)
A.$(0,4)$
B.$(2,0)$
C.$(-2,0)$
D.$(0,2)$

答案： B：$\because$一次函数$y = - 3x + b$的图象经过点$(1,3)$，$\therefore3=-3\times1 + b$，$\therefore b = 6$，$\therefore y = - 3x + 6$，当$y = 0$时，$-3x + 6 = 0$，$\therefore x = 2$，即一次函数$y = - 3x + 6$的图象与$x$轴的交点坐标为$(2,0)$。

3.(2024湖南衡阳衡山期末)函数$y = \frac{1}{x - 3} + \sqrt{x - 1}$的自变量x的取值范围是(M8204001) ( )
A.$x\geq1$
B.$x\geq1$且$x\neq3$
C.$x\neq3$
D.$1\leq x\leq3$

答案： B：由题意得$x - 1\geq0$且$x - 3\neq0$，$\therefore x\geq1$且$x\neq3$，故选B。

4.(2024湖南中考)对于一次函数$y = 2x - 1$,下列结论正确的是(M8204003) ( )
A.它的图象与y轴交于点$(0,-1)$
B.y随x的增大而减小
C.当$x＞\frac{1}{2}$时,$y＜0$
D.它的图象经过第一、二、三象限

答案： A：$\because$当$x = 0$时，$y = - 1$，$\therefore$它的图象与$y$轴交于点$(0,-1)$，故A选项正确；$\because2\gt0$，$-1\lt0$，$\therefore y$随$x$的增大而增大，且它的图象经过第一、三、四象限，故B、D选项错误；当$x\gt\frac{1}{2}$时，$y\gt0$，故C选项错误。故选A。

5.(2024湖南长沙开福模拟)直线$l_{1}:y = kx - b$和直线$l_{2}:y = -2kx + b$在同一平面直角坐标系中的图象可能是(M8204003) ( )

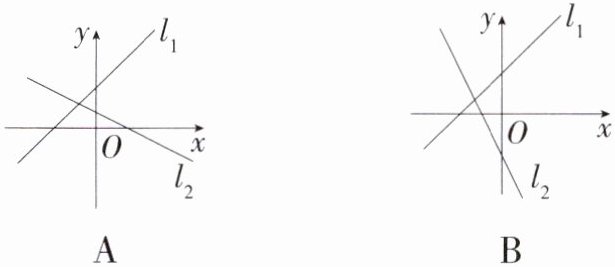
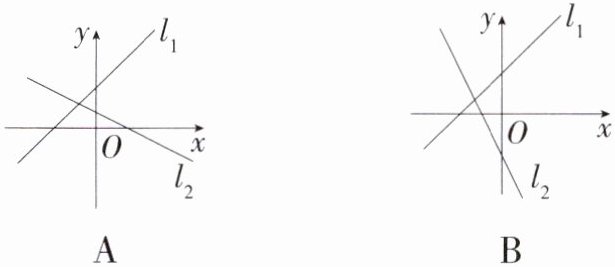
答案： B：\nA.直线$l_1:y = kx - b$中$k\gt0$，$b\lt0$，$l_2:y = - 2kx + b$中$k\gt0$，$b\gt0$，$b$的取值相矛盾，故本选项不符合题意；\nB.直线$l_1:y = kx - b$中$k\gt0$，$b\lt0$，$l_2:y = - 2kx + b$中$k\gt0$，$b\lt0$，$k$、$b$的取值一致，故本选项符合题意；\nC.直线$l_1:y = kx - b$中$k\lt0$，$b\lt0$，$l_2:y = - 2kx + b$中$k\gt0$，$b\lt0$，$k$的取值相矛盾，故本选项不符合题意；\nD.直线$l_1:y = kx - b$中$k\gt0$，$b\lt0$，$l_2:y = - 2kx + b$中$k\lt0$，$b\lt0$，$k$的取值相矛盾，故本选项不符合题意。故选B。

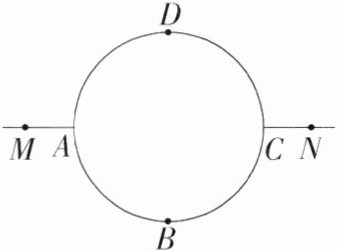
6.(2023河北中考)如图所示的是一种轨道示意图,其中弧ADC和弧ABC均为半圆,点M,A,C,N依次在同一直线上,且$AM = CN$.现有两个机器人(看成点)分别从M,N两点同时出发,沿着轨道以大小相同的速度匀速移动,其路线分别为$M\rightarrow A\rightarrow D\rightarrow C\rightarrow N$和$N\rightarrow C\rightarrow B\rightarrow A\rightarrow M$.若移动时间为x,两个机器人之间的距离为y,则y与x关系的图象大致是 ( )
            

答案： D：当两个机器人分别从$M$，$N$两点出发，未到圆弧上时，$y$随$x$的增大而减小，排除选项A和C；当两个机器人经过圆弧后，再分别在$CN$，$AM$上移动时，$y$随$x$的增大而增大，排除选项B，故选D。

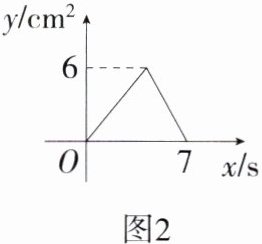
7.(2024四川广元中考)如图1,在$\triangle ABC$中,$\angle ACB = 90^{\circ}$,点P从点A出发沿$A\rightarrow C\rightarrow B$以1 cm/s的速度匀速运动至点B,图2是点P运动时,$\triangle ABP$的面积$y(cm^{2})$与时间$x(s)$之间的函数图象,则该三角形的斜边AB的长为 ( )
       
A.5
B.7
C.$3\sqrt{2}$
D.$2\sqrt{3}$

答案： A：当点$P$运动到$C$处时，$\triangle ABP$的面积取得最大值，为$6$，即$\frac{1}{2}AC\cdot BC = 6$，$\therefore AC\cdot BC = 12$。由题图2可知，点$P$从点$A$出发沿$A\rightarrow C\rightarrow B$以$1\mathrm{cm/s}$的速度匀速运动至点$B$的时间为$7\mathrm{s}$，即$AC + BC = 7$，$\therefore(AC + BC)^2 = 49$，即$AC^2 + BC^2 + 2AC\cdot BC = 49$，$\therefore AC^2 + BC^2 = 49 - 2\times12 = 25$，$\because AC^2 + BC^2 = AB^2$，$\therefore AB = 5$。故选A。