《2025年5年中考3年模拟八年级数学下册湘教版》

1. 若三条线段的长为a、b、c，且满足$a^{2}+b^{2}-c^{2}=0$，则这三条线段组成的三角形是 （ ）
A. 锐角三角形
B. 直角三角形
C. 钝角三角形
D. 无法判断

答案： B $\because a^{2}+b^{2}-c^{2}=0$，$\therefore a^{2}+b^{2}=c^{2}$，则这三条线段组成的三角形是直角三角形，故选 B.

2.（2024湖南长沙芙蓉模拟）下列各组数中，不能作为直角三角形的三边长的是 （ ）
A.$\sqrt{3}$，$\sqrt{4}$，$\sqrt{5}$
B. 6，8，10
C. 7，24，25
D.$\sqrt{34}$，3，5

答案： A A.$\because (\sqrt{3})^{2}+(\sqrt{4})^{2}\neq(\sqrt{5})^{2}$，$\therefore$ A 选项符合题意；B.$\because 6^{2}+8^{2}=10^{2}$，$\therefore$ B 选项不符合题意；C.$\because 7^{2}+24^{2}=25^{2}$，$\therefore$ C 选项不符合题意；D.$\because 3^{2}+5^{2}=(\sqrt{34})^{2}$，$\therefore$ D 选项不符合题意，故选 A.

3. 下列各组数中，是勾股数的是 （ ）
A.$\frac{1}{3}$，$\frac{1}{4}$，$\frac{1}{5}$
B. 0.3，0.4，0.5
C. 6，7，8
D. 5，12，13

答案： D A、B 选项中的数不是正整数，故不是勾股数；$6^{2}+7^{2}\neq8^{2}$，故 C 选项中的数不是勾股数；$5^{2}+12^{2}=13^{2}$，且 5，12，13 都是正整数，故 D 选项中的数是勾股数. 故选 D.

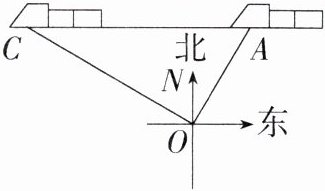
4. “淄博烧烤”火了，许多游客纷纷从外地来到淄博吃烧烤. 如图，南昌的小邦乘坐高铁从南昌到淄博去吃烧烤，在距离铁轨200米的O处，观察他所乘坐的由南昌经过淄博开往青岛的“和谐号”动车. 当“和谐号”动车车头在A处时，恰好位于O处的北偏东30°方向，测得OA = 300米，10秒钟后（该时段动车的平均速度是50米/秒），动车车头到达C处，测得OC = 400米. 根据所学知识求得此时点C位于点O的（M8201003）（ ）

A. 北偏西45°方向
B. 北偏西30°方向
C. 北偏西60°方向
D. 南偏东60°方向

答案： C $\because AC = 50\times10 = 500$ 米，$OA = 300$ 米，$OC = 400$ 米，$\therefore OC^{2}+OA^{2}=400^{2}+300^{2}=500^{2}=AC^{2}$，即 $OA^{2}+OC^{2}=AC^{2}$，$\therefore \triangle AOC$ 是直角三角形，且 $\angle AOC = 90^{\circ}$.$\because \angle AON = 30^{\circ}$，$\therefore \angle CON = 60^{\circ}$，即点 C 位于点 O 的北偏西 $60^{\circ}$ 方向.

5. 如果一个三角形的三边长分别为3，4，5，那么这个三角形的面积为________.（M8201003）

答案： 答案 6
解析 $\because 3^{2}+4^{2}=25 = 5^{2}$，$\therefore$ 这个三角形是直角三角形，且 3，4 为两条直角边的长.$\therefore$ 这个三角形的面积 $=\frac{1}{2}\times3\times4 = 6$.

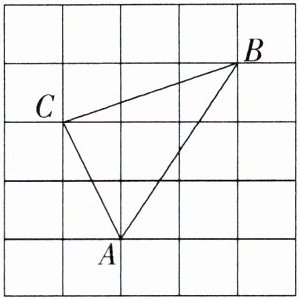
6. 如图，网格中小正方形的边长均为1，△ABC的三个顶点都在小正方形的顶点上. 请判断△ABC是不是直角三角形，并说明理由.

答案： 解析 $\triangle ABC$ 不是直角三角形.
理由：由题意得 $AC^{2}=1^{2}+2^{2}=5$，$AB^{2}=2^{2}+3^{2}=13$，$BC^{2}=1^{2}+3^{2}=10$，$\because AC^{2}+BC^{2}\neq AB^{2}$，$\therefore \triangle ABC$ 不是直角三角形.

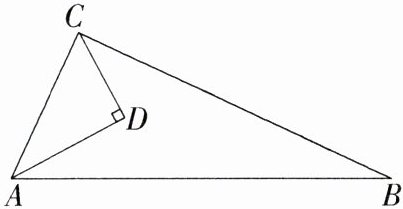
7. 教材变式·P16T3（2023湖南株洲攸县期中）如图，AD = 4，CD = 3，AB = 13，BC = 12，∠ADC = 90°，求△ABC的面积.（M8201003）

答案： 解析 $\because AD = 4$，$CD = 3$，$\angle ADC = 90^{\circ}$，$\therefore AC=\sqrt{AD^{2}+CD^{2}}=\sqrt{4^{2}+3^{2}} = 5$，在 $\triangle ABC$ 中，$AC = 5$，$AB = 13$，$BC = 12$，$\because 5^{2}+12^{2}=13^{2}$，$\therefore AC^{2}+BC^{2}=AB^{2}$，$\therefore \triangle ABC$ 为直角三角形，$\angle ACB = 90^{\circ}$，$\therefore S_{\triangle ABC}=\frac{1}{2}\times5\times12 = 30$.

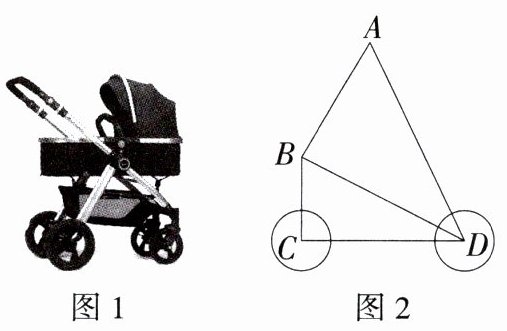
8.（2024广西南宁兴宁月考）图1是某品牌婴儿车，图2为其简化结构示意图. 根据安全标准，该车需满足BC⊥CD，现测得AB = CD = 6 dm，BC = 3 dm，AD = 9 dm，其中AB与BD之间由一个固定为90°的零件连接（即∠ABD = 90°），请通过计算说明该婴儿车是否符合安全标准.
                                                                                                        

答案： 解析 在 $Rt\triangle ABD$ 中，$BD^{2}=AD^{2}-AB^{2}=9^{2}-6^{2}=45$，在 $\triangle BCD$ 中，$BC^{2}+CD^{2}=3^{2}+6^{2}=45$，$\therefore BC^{2}+CD^{2}=BD^{2}$，$\therefore \angle BCD = 90^{\circ}$，$\therefore BC\perp CD$. 故该婴儿车符合安全标准.