《2025年5年中考3年模拟八年级数学下册湘教版》

7.(2023湖南邵阳期末,10,★☆☆)如图,点B、D、E在同一条直线上,AB⊥BC,AD⊥BE,CE⊥BE,AB = BC,AD = 7,CE = 4,则DE的长为 ( )

A.2
B.3
C.4
D.7

答案： B
$\because AB\perp BC,AD\perp BE,CE\perp BE,\therefore\angle ABC=\angle ADB=\angle BEC = 90^{\circ}$，$\therefore\angle BAD+\angle ABD = 90^{\circ},\angle CBE+\angle ABD = 90^{\circ}$，$\therefore\angle BAD=\angle CBE$，在$\triangle ABD$与$\triangle BCE$中，$\begin{cases}\angle ADB=\angle BEC,\\\angle BAD=\angle CBE,\\AB = BC,\end{cases}\therefore\triangle ABD\cong\triangle BCE(AAS)$，
$\therefore BE = AD = 7,BD = CE = 4,\therefore DE = BE - BD = 3$.故选 B.

8.(2024湖南湘潭期中,16,★☆☆)如图,D是Rt△ABC中斜边BC上的一点,且BD = AB,过D作BC的垂线,交AC于点E.若AE = 5 cm,DC = 12 cm,则CE的长为 ________cm(M8201004).

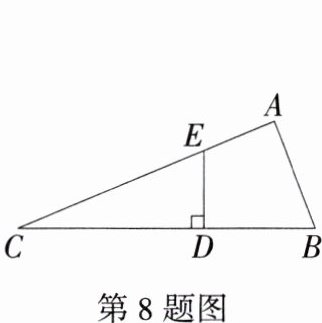
答案：
答案 13
解析 如图，连接$BE$，由题意知$DE\perp BC$，
$\therefore\angle EDC = 90^{\circ},\angle EDB=\angle A = 90^{\circ}$，
在$Rt\triangle EDB$和$Rt\triangle EAB$中，$\begin{cases}BE = BE,\\BD = AB,\end{cases}$
$\therefore Rt\triangle EDB\cong Rt\triangle EAB(HL)$，$\therefore DE = AE = 5\ cm$，
在$Rt\triangle EDC$中，$ED = 5\ cm,DC = 12\ cm$，由勾股定理得$CE=\sqrt{ED^{2}+CD^{2}} = 13\ cm$.

9.(2024湖南邵阳新宁期中,26,★★☆)如图,在△ABC中,AB = AC,DE是过点A的直线,BD⊥DE于点D,CE⊥DE于点E.
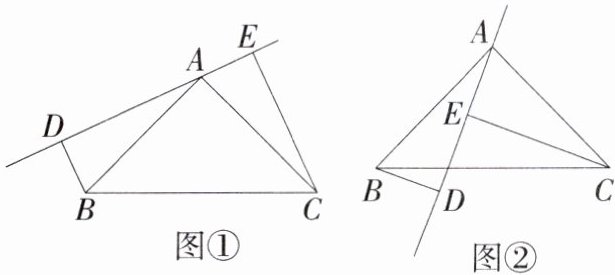
(1)若B、C在DE的同侧(如图①所示)且AD = CE,求证:AB⊥AC.
(2)若B、C在DE的两侧(如图②所示)且AD = CE,其他条件不变,AB与AC还垂直吗?若垂直,请给出证明;若不垂直,请说明理由.

答案： 解析
(1) 证明：$\because BD\perp DE,CE\perp DE$，
$\therefore\angle ADB=\angle AEC = 90^{\circ}$，
在$Rt\triangle ABD$和$Rt\triangle CAE$中，$\begin{cases}AB = CA,\\AD = CE,\end{cases}$
$\therefore Rt\triangle ABD\cong Rt\triangle CAE(HL)$.
$\therefore\angle DBA=\angle EAC$.
$\because\angle DAB+\angle DBA = 90^{\circ},\therefore\angle DAB+\angle EAC = 90^{\circ}$.
$\because\angle BAC = 180^{\circ}-(\angle DAB+\angle EAC)=90^{\circ},\therefore AB\perp AC$.
(2)$AB\perp AC$.
证明：由
(1)同理可证$Rt\triangle ABD\cong Rt\triangle CAE$，
$\therefore\angle DAB=\angle ECA$，
$\because\angle CAE+\angle ECA = 90^{\circ}$，
$\therefore\angle CAE+\angle DAB = 90^{\circ}$，即$\angle BAC = 90^{\circ},\therefore AB\perp AC$.

10.模型观念 如图①,AB = 4 cm,AC⊥AB于点A,BD⊥AB于点B,AC = BD = 3 cm.点P在线段AB上以1 cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t s.(M8201004)
(1)若点Q的运动速度与点P的运动速度相等,当t = 1时,△ACP与△BPQ是否全等?请说明理由,并判断此时线段PC和线段PQ的位置关系.
(2)如图②,将题干中的“AC⊥AB于点A,BD⊥AB于点B”改为“∠CAB = ∠DBA = 60°”,其他条件不变,设点Q的运动速度为x cm/s,是否存在实数x,使得△ACP与△BPQ全等?若存在,请求出相应的x、t的值;若不存在,请说明理由.

答案： 解析
(1)$\triangle ACP\cong\triangle BPQ$.理由如下：
当$t = 1$时，$AP = BQ = 1\ cm$，$\therefore BP = 3\ cm = AC$，
在$\triangle ACP$和$\triangle BPQ$中，$\begin{cases}AP = BQ,\\\angle A=\angle B = 90^{\circ},\\AC = BP,\end{cases}$
$\therefore\triangle ACP\cong\triangle BPQ(SAS)$，
$\therefore\angle ACP=\angle BPQ$，
$\therefore\angle APC+\angle BPQ=\angle APC+\angle ACP = 90^{\circ}$，
$\therefore\angle CPQ = 90^{\circ}$，即线段$PC$与线段$PQ$垂直.
(2) 存在.
①若$\triangle ACP\cong\triangle BPQ$，则$AC = BP,AP = BQ$，
$\therefore\begin{cases}3 = 4 - t,\\t = xt,\end{cases}$解得$\begin{cases}t = 1,\\x = 1;\end{cases}$
②若$\triangle ACP\cong\triangle BQP$，则$AC = BQ,AP = BP$，
$\therefore\begin{cases}3 = xt,\\t = 4 - t,\end{cases}$解得$\begin{cases}t = 2,\\x=\frac{3}{2}.\end{cases}$
综上所述，当$\begin{cases}t = 1,\\x = 1\end{cases}$或$\begin{cases}t = 2,\\x=\frac{3}{2}\end{cases}$时，$\triangle ACP$与$\triangle BPQ$全等.