《2025年5年中考3年模拟八年级数学下册湘教版》

1. 下列说法中，能确定物体位置的是 ( )
A. 天空中的一只小鸟
B. 电影院中18座
C. 东经118°，北纬40°
D. 北偏西35°方向

答案： 确定一个物体具体的位置通常需要两个量，故满足题意的只有C选项.

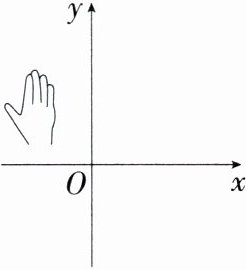
2.(2024贵州铜仁一模)如图，小明用手盖住的点的坐标可能为 ( )

A. (3,2)
B. (-3,2)
C. (3,-2)
D. (-3,-2)

答案： 由题图可知，小手盖住的点在第二象限，且第二象限内的点的横坐标为负数，纵坐标为正数，故选B.

3.(2024广西贺州期末)已知点A(m - 1,3)与点B(2,n - 1)关于x轴对称，则(m + n)^{2025}的值为 ( )
A. 0
B. 1
C. -1
D. 3^{2025}

答案：
∵点A(m - 1,3)与点B(2,n - 1)关于x轴对称，
∴m - 1 = 2，n - 1 = - 3，
∴m = 3，n = - 2，
∴(m + n)^{2025}=(3 - 2)^{2025}=1，故选B.

4. 易错题(2024湖南娄底月考)在平面直角坐标系中，第二象限内有一点M到x轴的距离为5，到y轴的距离为6，则点M的坐标是 ( )
A. (-5,6)
B. (5,-6)
C. (-6,5)
D. (6,-5)

答案： 设点M的坐标是(x,y)，
∵点M到x轴的距离为5，到y轴的距离为6，
∴|y| = 5，|x| = 6.又
∵点M在第二象限内，
∴x = - 6，y = 5，
∴点M的坐标为(- 6,5)，故选C.
·易错警示
平面上一点到坐标轴的距离与点的坐标有关，熟记点到x轴的距离为点的纵坐标的绝对值，到y轴的距离为点的横坐标的绝对值，避免把横、纵坐标的位置写颠倒，本题还易因忽略各象限内点的坐标的符号特征而出现错误.

5. 新独家原创 如图，△DCE是△OAB沿x轴正方向平移得到的，已知A，B两点的坐标分别为(2,5)，(6,0)，若OE = 8，则点C的坐标为 ( )

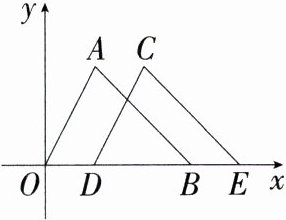
A. (4,5)
B. (6,5)
C. (6,2)
D. (2,7)

答案：
∵B(6,0)，
∴OB = 6，
∵OE = 8，
∴BE = OE - OB = 2，
∴△OAB沿x轴正方向平移2个单位得到△DCE，
∴点C是将点A向右平移2个单位得到的，
∴点C的坐标是(4,5).故选A.

6. 情境题·国家安全(2022浙江台州中考改编)中国自主研发的“歼 - 20”战机是最新一代双发重型隐形战斗机，它将负担中国空军未来对空、对海的主权维护任务. 下图是战机在空中展示的轴对称队形，以战机B，C所在直线为x轴、队形的对称轴为y轴，建立平面直角坐标系. 若战机E的坐标为(40,a)，则战机D的坐标为 ( )

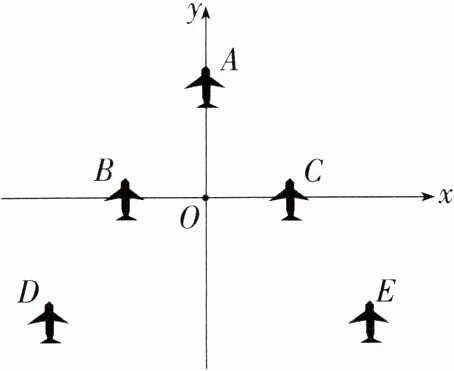
A. (40,-a)
B. (-40,a)
C. (-40,-a)
D. (a,-40)

答案：
∵战机E与战机D关于y轴对称，且战机E的坐标为(40,a)，
∴战机D的坐标为(- 40,a)，故选B.

7. 在平面直角坐标系中，点P(m - 2,m + 1)一定不在的象限为 ( )
A. 第四象限
B. 第三象限
C. 第二象限
D. 第一象限

答案：
∵(m + 1)-(m - 2)=m + 1 - m + 2 = 3，
∴点P的纵坐标大于横坐标，
∴点P一定不在第四象限.故选A.

8. 如图，在平面直角坐标系中，存在三个定点分别为A(-2,-2)，B(6,-2)，C(6,4). 现添加一点D，使得AD = 5，那么CD的长不可能为 ( )

A. 4
B. 7
C. 11
D. 15

答案： 由题意得，AC = $\sqrt{AB^{2}+BC^{2}}=\sqrt{[6 - (- 2)]^{2}+[4 - (- 2)]^{2}}$ = 10.当点D在AC上时，CD取得最小值，最小值为10 - 5 = 5，
∴CD的长不可能是4，故选A.

9. 跨体育与健康·冰壶 冰壶被喻为冰上的“国际象棋”，它考验参与者的体能与脑力，展现动静之美，取舍之智慧，属于冬奥会比赛项目，冰壶运动的计分方法：图中最大圆及其内部为有效圈，点P为有效圈中心；一队每颗位于有效圈中且位置较另一队所有冰壶都更接近点P的冰壶皆可获计一分. 在图中，分别以水平向右、竖直向上的方向为x轴、y轴的正方向建立平面直角坐标系，下列选项对各冰壶位置描述正确的是 ( )

A. 若得分壶A的坐标为(0,1)，得分壶B的坐标为(1,2)，则冰壶C的坐标约为(0.5,4)
B. 若得分壶A的坐标为(0,-2)，得分壶B的坐标为(2,0)，则冰壶C的坐标约为(3,3)
C. 若得分壶A的坐标为(-2,0)，得分壶B的坐标为(0,2)，则冰壶C的坐标约为(1,8)
D. 若得分壶A的坐标为(0,0)，得分壶B的坐标为(1,1)，则冰壶C的坐标约为(4,1.5)

答案： A.若得分壶A的坐标为(0,1)，得分壶B的坐标为(1,2)，则冰壶C的坐标约为(1.5,5)，故本选项不符合题意；B.若得分壶A的坐标为(0,- 2)，得分壶B的坐标为(2,0)，则冰壶C的坐标约为(3,6)，故本选项不符合题意；C.若得分壶A的坐标为(- 2,0)，得分壶B的坐标为(0,2)，则冰壶C的坐标约为(1,8)，故本选项符合题意；D.若得分壶A的坐标为(0,0)，得分壶B的坐标为(1,1)，则冰壶C的坐标约为(1.5,4)，故本选项不符合题意.故选C.