第22页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
10.(2024湖南长沙一模,14,★★☆)如图,CE,CF是正六边形的两条对角线,则∠ECF的大小为________.


答案:
**答案** 30°
**解析**
∵多边形是正六边形,
∴∠D = ∠B = ∠BCD = $\frac{(6 - 2)×180°}{6}$ = 120°,CD = DE,
∴∠DCE = ∠DEC = $\frac{1}{2}$×(180° - 120°) = 30°,连接 AC(图略),易证△ABC≌△EDC,
∴∠ACB = ∠DCE = 30°,AC = CE,结合 AF = EF,CF = CF 可证△ACF≌△ECF,
∴∠ECF = ∠ACF = $\frac{1}{2}$×(120° - 30°×2) = 30°.
**解析**
∵多边形是正六边形,
∴∠D = ∠B = ∠BCD = $\frac{(6 - 2)×180°}{6}$ = 120°,CD = DE,
∴∠DCE = ∠DEC = $\frac{1}{2}$×(180° - 120°) = 30°,连接 AC(图略),易证△ABC≌△EDC,
∴∠ACB = ∠DCE = 30°,AC = CE,结合 AF = EF,CF = CF 可证△ACF≌△ECF,
∴∠ECF = ∠ACF = $\frac{1}{2}$×(120° - 30°×2) = 30°.
11.(2022四川遂宁中考,13,★★☆)如图,正六边形ABCDEF的顶点A、F分别在正方形BMGH的边BH、GH上.若正方形BMGH的边长为6,则正六边形ABCDEF的边长为________.


答案:
**答案** 4
**解析** 设 AF = x,则 AB = x,AH = 6 - x,
∵六边形 ABCDEF 是正六边形,
∴∠BAF = 120°,
∴∠HAF = 60°,
∵∠AHF = 90°,
∴∠AFH = 30°,
∴AF = 2AH,
∴x = 2(6 - x),解得 x = 4,即正六边形 ABCDEF 的边长为 4.
**解析** 设 AF = x,则 AB = x,AH = 6 - x,
∵六边形 ABCDEF 是正六边形,
∴∠BAF = 120°,
∴∠HAF = 60°,
∵∠AHF = 90°,
∴∠AFH = 30°,
∴AF = 2AH,
∴x = 2(6 - x),解得 x = 4,即正六边形 ABCDEF 的边长为 4.
12.(2024湖南长沙雨花一模,16,★★☆)小明用一些完全相同的三角形纸片(图中△ABC)拼接图案,已知用6个△ABC纸片按照如图1所示的方法拼接可得外轮廓是正六边形的图案,若按照如图2所示的方法拼接下去,则得到的图案的外轮廓是正________边形.


答案:
**答案** 九
**解析**
∵正六边形的每一个内角为 120°,
∴∠ACB = 120° - 80° = 40°,
∴∠CAB = 180° - ∠ABC - ∠ACB = 60°,
∴题图 2 中正多边形的每一个内角为 60° + 80° = 140°,每一个外角为 180° - 140° = 40°,360°÷40° = 9,即图案的外轮廓是正九边形.
**解析**
∵正六边形的每一个内角为 120°,
∴∠ACB = 120° - 80° = 40°,
∴∠CAB = 180° - ∠ABC - ∠ACB = 60°,
∴题图 2 中正多边形的每一个内角为 60° + 80° = 140°,每一个外角为 180° - 140° = 40°,360°÷40° = 9,即图案的外轮廓是正九边形.
13.易错题(2023湖南永州九中月考,13,★★☆)一个多边形的外角和是其内角和的\frac{2}{5},若这个多边形截去一个角,则所形成的多边形是________边形.(M8202001)
答案:
**答案** 六或七或八
**解析** 设原多边形的边数为 n,依题意,得$\frac{2}{5}$(n - 2)×180° = 360°,解得 n = 7.
如图,截去一个角有三种情况:
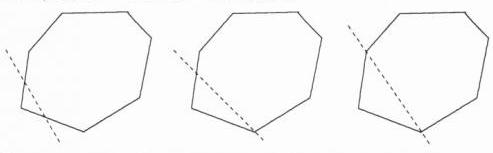
①不经过顶点截,则所形成的多边形是八边形;
②只过一个顶点截,则所形成的多边形是七边形;
③过两个顶点截,则所形成的多边形是六边形.
**易错警示**
解题时容易因考虑问题不全面而出错,应注意这个多边形截去一个角有三种情况.
**答案** 六或七或八
**解析** 设原多边形的边数为 n,依题意,得$\frac{2}{5}$(n - 2)×180° = 360°,解得 n = 7.
如图,截去一个角有三种情况:

①不经过顶点截,则所形成的多边形是八边形;
②只过一个顶点截,则所形成的多边形是七边形;
③过两个顶点截,则所形成的多边形是六边形.
**易错警示**
解题时容易因考虑问题不全面而出错,应注意这个多边形截去一个角有三种情况.
14.运算能力(2024湖南怀化新晃期中)利用“模型”解决几何综合问题往往会取得事半功倍的效果.
几何模型:如图1,我们称它为“A”形图,易证明:∠EDF = ∠A + ∠B + ∠C.
应用上面模型结论解决问题:
(1)如图2,“五角星”中,求∠A₁ + ∠A₂ + ∠A₃ + ∠A₄ + ∠A₅的值.
分析:图中四边形A₁A₃DA₄是“A”形图,于是有∠A₂DA₅ = ∠A₁ + ∠A₃ + ∠A₄,所以∠A₁ + ∠A₂ + ∠A₃ + ∠A₄ + ∠A₅ = ________.
(2)如图3,“七角星”中,求∠A₁ + ∠A₂ + ∠A₃ + ∠A₄ + ∠A₅ + ∠A₆ + ∠A₇的值.
(3)如图4,“八角星”中,∠A₁ + ∠A₂ + ∠A₃ + ∠A₄ + ∠A₅ + ∠A₆ + ∠A₇ + ∠A₈ = ________.
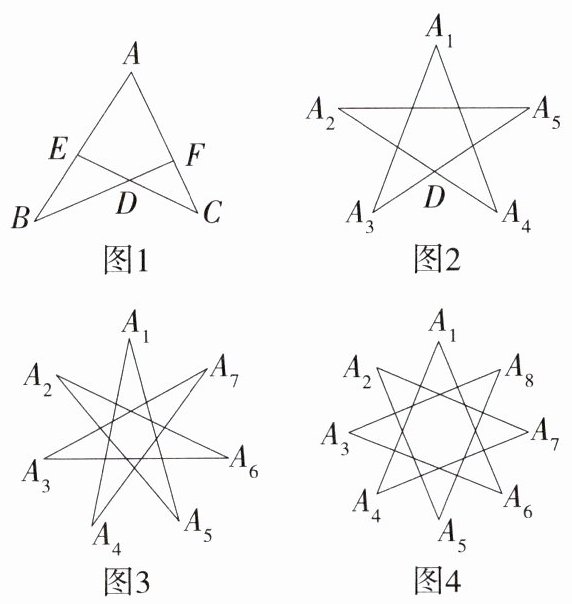
几何模型:如图1,我们称它为“A”形图,易证明:∠EDF = ∠A + ∠B + ∠C.
应用上面模型结论解决问题:
(1)如图2,“五角星”中,求∠A₁ + ∠A₂ + ∠A₃ + ∠A₄ + ∠A₅的值.
分析:图中四边形A₁A₃DA₄是“A”形图,于是有∠A₂DA₅ = ∠A₁ + ∠A₃ + ∠A₄,所以∠A₁ + ∠A₂ + ∠A₃ + ∠A₄ + ∠A₅ = ________.
(2)如图3,“七角星”中,求∠A₁ + ∠A₂ + ∠A₃ + ∠A₄ + ∠A₅ + ∠A₆ + ∠A₇的值.
(3)如图4,“八角星”中,∠A₁ + ∠A₂ + ∠A₃ + ∠A₄ + ∠A₅ + ∠A₆ + ∠A₇ + ∠A₈ = ________.

答案:
**解析**
(1)180°.
(2)如图,

∵图中四边形 A₁A₄EA₅ 和四边形 A₆A₂FA₃ 都是“A”形图,
∴∠A₂EA₇ = ∠A₁ + ∠A₄ + ∠A₅,∠A₅FA₇ = ∠A₂ + ∠A₃ + ∠A₆,
在三角形 A₇EF 中,
∵∠A₇ + ∠A₂EA₇ + ∠A₅FA₇ = 180°,
∴∠A₁ + ∠A₂ + ∠A₃ + ∠A₄ + ∠A₅ + ∠A₆ + ∠A₇ = 180°.
(3)如图,

∵图中四边形 A₁A₄EA₆ 和四边形 A₂A₅FA₇ 都是“A”形图,
∴∠A₁ + ∠A₄ + ∠A₆ = ∠A₃EA₇,
∠A₂ + ∠A₅ + ∠A₇ = ∠A₄FA₈,
在四边形 A₃EFA₈ 中,
∵∠A₃ + ∠A₈ + ∠A₃EA₇ + ∠A₄FA₈ = 360°,
∴∠A₁ + ∠A₂ + ∠A₃ + ∠A₄ + ∠A₅ + ∠A₆ + ∠A₇ + ∠A₈ = 360°.
故答案为 360°.
**解析**
(1)180°.
(2)如图,

∵图中四边形 A₁A₄EA₅ 和四边形 A₆A₂FA₃ 都是“A”形图,
∴∠A₂EA₇ = ∠A₁ + ∠A₄ + ∠A₅,∠A₅FA₇ = ∠A₂ + ∠A₃ + ∠A₆,
在三角形 A₇EF 中,
∵∠A₇ + ∠A₂EA₇ + ∠A₅FA₇ = 180°,
∴∠A₁ + ∠A₂ + ∠A₃ + ∠A₄ + ∠A₅ + ∠A₆ + ∠A₇ = 180°.
(3)如图,

∵图中四边形 A₁A₄EA₆ 和四边形 A₂A₅FA₇ 都是“A”形图,
∴∠A₁ + ∠A₄ + ∠A₆ = ∠A₃EA₇,
∠A₂ + ∠A₅ + ∠A₇ = ∠A₄FA₈,
在四边形 A₃EFA₈ 中,
∵∠A₃ + ∠A₈ + ∠A₃EA₇ + ∠A₄FA₈ = 360°,
∴∠A₁ + ∠A₂ + ∠A₃ + ∠A₄ + ∠A₅ + ∠A₆ + ∠A₇ + ∠A₈ = 360°.
故答案为 360°.
查看更多完整答案,请扫码查看


