《2025年5年中考3年模拟八年级数学下册湘教版》

1.(2024广西南宁兴宁期中)下列函数中,是正比例函数的是(M8204002) ( )
A.$y = 2x^{2}$
B.$y = \frac{8}{x}$
C.$y = 6x$
D.$y = 3x - 2$

答案： C 正比例函数的一般形式为 $y = kx$（$k$ 为常数，且 $k\neq0$），符合这一形式的只有 $y = 6x$. 故选 C.

2.(2024贵州遵义一模)下列函数中,$y$是$x$的一次函数的是(M8204003) ( )
A.$y = \frac{3}{x}$
B.$y = 2x^{2} + 3x - 1$
C.$y = x - 1$
D.$y = x^{2} - 1$

答案： C \nA. $\because$ 分母中含有自变量 $x$，$\therefore y=\frac{3}{x}$ 不是一次函数；\nB. $\because$ 自变量 $x$ 的最高次数为 2，$\therefore y = 2x^{2}+3x - 1$ 不是一次函数；\nC. $y = x - 1$ 是一次函数；\nD. $\because$ 自变量 $x$ 的次数为 2，$\therefore y = x^{2}-1$ 不是一次函数. 故选 C.

3.易错题 如果函数$y = (k - 2)x^{|k - 1|}$是关于$x$的正比例函数,那么$k$的值为 ( )
A.0
B.1
C.0或2
D.2

答案： A 由题意得 $|k - 1| = 1$ 且 $k - 2\neq0$，$\therefore k = 0$，故选 A.

4.教材变式·P120习题T1 下列给出的几个函数关系中,成正比例函数关系的是(M8204002) ( )
A.矩形面积固定,长和宽的关系
B.正方形的面积和边长之间的关系
C.三角形的面积一定,底边和底边上的高之间的关系
D.匀速运动中,路程和时间的关系

答案： D \nA. 矩形面积固定，长 $=\frac{面积}{宽}$，$\therefore$ 长和宽不成正比例函数关系；\nB. 正方形的面积 = 边长的平方，$\therefore$ 正方形的面积和边长不成正比例函数关系；\nC. 底边 $=\frac{2\times 三角形的面积}{底边上的高}$，$\therefore$ 底边和底边上的高不成正比例函数关系；\nD. 路程 = 速度 $\times$ 时间，$\therefore$ 匀速运动中，路程和时间成正比例函数关系. 故选 D.

5.若函数$y = (6 + 3m)x + n$是关于$x$的一次函数,则$m$应满足的条件是_______.

答案： 答案：$m\neq - 2$
**解析**：$\because$ 函数 $y=(6 + 3m)x + n$ 是关于 $x$ 的一次函数，$\therefore 6 + 3m\neq0$，解得 $m\neq - 2$.

6.新独家原创 《中华人民共和国道路交通安全法》规定,同车道行驶的机动车,后车应当与前车保持足以采取紧急制动措施的安全距离,某汽车公司为确定一款新能源汽车在高速公路上紧急刹车后滑行的距离$s$(单位:m)与刹车时的速度$v$(单位:km/h)(车速不超过120 km/h)的函数关系,对这种型号的新能源汽车进行了测试,测得的数据如表:

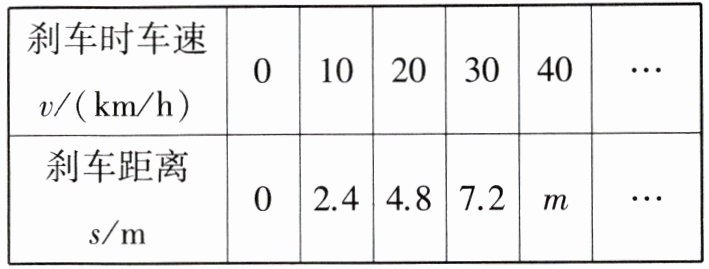
变量$s$与$v$之间的函数关系式是_______.

答案： 答案：$s = 0.24v(0\leq v\leq120)$
**解析**：由表格中数据变化规律可知，刹车时车速每增加 $10\ km/h$，刹车距离增加 $2.4\ m$，$\therefore$ 刹车距离 $s$ 与刹车时车速 $v$ 的函数关系式为 $s = 0.24v(0\leq v\leq120)$.

7.求下列各题中$y$与$x$之间的函数表达式,并判断$y$是不是$x$的一次函数或正比例函数.
(1)某农场种植玉米,每平方米种植玉米6株,玉米株数$y$与种植面积$x(m^{2})$之间的关系.
(2)等腰三角形$ABC$的周长为16 cm,底边$BC$长为$y$ cm,腰$AB$长为$x$ cm,$y$与$x$之间的关系.
(3)圆柱的底面圆的面积为2 cm²,它的体积$y(cm^{3})$与圆柱的高$x$(cm)之间的关系.
(4)一棵小树现在的高度为80 cm,以后每年长高20 cm,$x$年后,小树的高度$y$(cm)与生长的年数$x$的关系.

答案： 解析：\n
(1) 由题知，$y = 6x$，所以 $y$ 是 $x$ 的正比例函数.\n
(2) 由题知，$y=-2x + 16$，所以 $y$ 是 $x$ 的一次函数.\n
(3) 由题知，$y = 2x$，所以 $y$ 是 $x$ 的正比例函数.\n
(4) 由题知，$y = 20x + 80$，所以 $y$ 是 $x$ 的一次函数.

8.已知函数$y = (m - 10)x + 1 - 2m$.
(1)当$m$满足什么条件时,这个函数是关于$x$的一次函数?
(2)当$m$满足什么条件时,这个函数是关于$x$的正比例函数?

答案： 解析：\n
(1) 根据一次函数的定义，可得 $m - 10\neq0$，$\therefore m\neq10$，故当 $m\neq10$ 时，这个函数是关于 $x$ 的一次函数.\n
(2) 根据正比例函数的定义，可得 $m - 10\neq0$ 且 $1 - 2m = 0$，$\therefore m=\frac{1}{2}$，故当 $m=\frac{1}{2}$ 时，这个函数是关于 $x$ 的正比例函数.