第30页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
7.(2024湖南长沙岳麓模拟,15,★☆☆)如图,$\triangle DEC$与$\triangle ABC$关于点$C$成中心对称,若$AB = 3$,$AC = 1$,$\angle D = 90^{\circ}$,则$AE$的长是______.


答案:
答案 $\sqrt{13}$
解析
∵ △DEC 与 △ABC 关于点 C 成中心对称,
∴ △ABC≌△DEC,
∴ AB = DE = 3,AC = DC = 1,
∴ AD = 2,
∵ ∠D = 90°,
∴ $AE=\sqrt{DE^{2}+AD^{2}}=\sqrt{3^{2}+2^{2}}=\sqrt{13}$.
解析
∵ △DEC 与 △ABC 关于点 C 成中心对称,
∴ △ABC≌△DEC,
∴ AB = DE = 3,AC = DC = 1,
∴ AD = 2,
∵ ∠D = 90°,
∴ $AE=\sqrt{DE^{2}+AD^{2}}=\sqrt{3^{2}+2^{2}}=\sqrt{13}$.
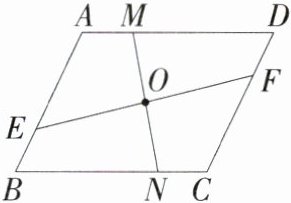
8.(2024陕西咸阳三模,13,★☆☆)如图,在平行四边形$ABCD$中,$AB = 6$,$BC = 8$,线段$EF$与线段$MN$相交于平行四边形$ABCD$的对称中心$O$,且将平行四边形$ABCD$的面积分成相等的四份,若$AM = 2$,则$BE =$______.

答案:
答案 $\frac{3}{2}$
解析 如图,连接 AC,BD,
∵ 点 O 为平行四边形 ABCD 的对称中心,
∴ AC 与 BD 相交于点 O.
∵ AC 与 BD 是平行四边形 ABCD 的对角线,
∴ $S_{\triangle AOB}=S_{\triangle AOD}=\frac{1}{4}S_{平行四边形ABCD}$.
过点 O 分别作 AB,AD 的垂线,垂足分别为 P,Q,
∴ $\frac{1}{2}AB\cdot OP=\frac{1}{2}AD\cdot OQ$.
∵ AB = 6,AD = BC = 8,
∴ 3OP = 4OQ,
∴ $\frac{OQ}{OP}=\frac{3}{4}$.
∵ 线段 MN 与线段 EF 将平行四边形 ABCD 的面积分成相等的四份,
∴ $S_{\triangle AOB}=S_{四边形AEOM}$,
即 $S_{\triangle AOE}+S_{\triangle BOE}=S_{\triangle AOE}+S_{\triangle AOM}$,
∴ $S_{\triangle BOE}=S_{\triangle AOM}$,
∴ $\frac{1}{2}BE\cdot OP=\frac{1}{2}AM\cdot OQ$,
∴ $BE=\frac{OQ}{OP}\cdot AM=\frac{3}{4}\times2=\frac{3}{2}$.

答案 $\frac{3}{2}$
解析 如图,连接 AC,BD,
∵ 点 O 为平行四边形 ABCD 的对称中心,
∴ AC 与 BD 相交于点 O.
∵ AC 与 BD 是平行四边形 ABCD 的对角线,
∴ $S_{\triangle AOB}=S_{\triangle AOD}=\frac{1}{4}S_{平行四边形ABCD}$.
过点 O 分别作 AB,AD 的垂线,垂足分别为 P,Q,
∴ $\frac{1}{2}AB\cdot OP=\frac{1}{2}AD\cdot OQ$.
∵ AB = 6,AD = BC = 8,
∴ 3OP = 4OQ,
∴ $\frac{OQ}{OP}=\frac{3}{4}$.
∵ 线段 MN 与线段 EF 将平行四边形 ABCD 的面积分成相等的四份,
∴ $S_{\triangle AOB}=S_{四边形AEOM}$,
即 $S_{\triangle AOE}+S_{\triangle BOE}=S_{\triangle AOE}+S_{\triangle AOM}$,
∴ $S_{\triangle BOE}=S_{\triangle AOM}$,
∴ $\frac{1}{2}BE\cdot OP=\frac{1}{2}AM\cdot OQ$,
∴ $BE=\frac{OQ}{OP}\cdot AM=\frac{3}{4}\times2=\frac{3}{2}$.

9.(2024浙江宁波期中,19,★★☆)如图,4个全等的正方形组成L形图案,请按下列要求画图(画出一种可能的情况即可):
(1)在图1中添加1个正方形,使它是轴对称图形,但不是中心对称图形.
(2)在图2中添加1个正方形,使它是中心对称图形,但不是轴对称图形.
(3)在图3中改变1个正方形的位置,从而得到一个新图形,使它既是中心对称图形,又是轴对称图形.
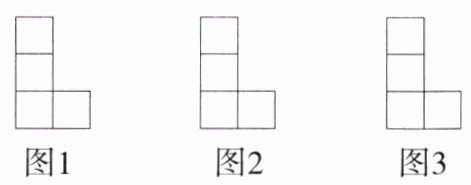
(1)在图1中添加1个正方形,使它是轴对称图形,但不是中心对称图形.
(2)在图2中添加1个正方形,使它是中心对称图形,但不是轴对称图形.
(3)在图3中改变1个正方形的位置,从而得到一个新图形,使它既是中心对称图形,又是轴对称图形.

答案:
解析
(1) 如图①、图②、图③所示(画出其中一种图即可).

(2) 如图④所示.
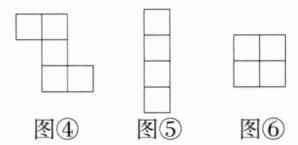
(3) 如图⑤、图⑥所示(画出其中一种图即可).
解析
(1) 如图①、图②、图③所示(画出其中一种图即可).

(2) 如图④所示.

(3) 如图⑤、图⑥所示(画出其中一种图即可).
10.(2023贵州遵义模拟,20,★★☆)如图,在$Rt\triangle ABC$中,$\angle BAC = 90^{\circ}$,$AD$是$BC$边上的中线,$E$是$AD$的中点,点$F$与点$B$关于点$E$对称,连接$AF,DF$.
(1)求证:四边形$ABDF$是平行四边形.
(2)写出一个与$\triangle ABD$面积相等的三角形:______.
(3)若$AC = 6$,$AB = 8$,求$\triangle BDF$的面积.
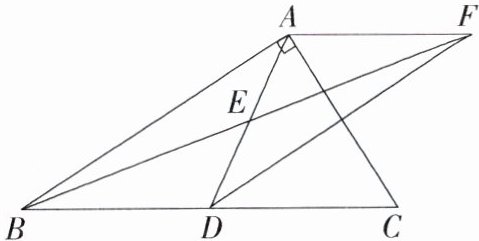
(1)求证:四边形$ABDF$是平行四边形.
(2)写出一个与$\triangle ABD$面积相等的三角形:______.
(3)若$AC = 6$,$AB = 8$,求$\triangle BDF$的面积.

答案:
解析
(1) 证明:
∵ E 是 AD 的中点,点 F 与点 B 关于点 E 对称,
∴ AE = DE,BE = EF,
∴ 四边形 ABDF 是平行四边形.
(2) △BDF(答案不唯一).
(3) 过点 A 作 AG⊥BC 于点 G,如图所示,
∵ ∠BAC = 90°,AC = 6,AB = 8,
∴ $BC=\sqrt{AB^{2}+AC^{2}}=\sqrt{8^{2}+6^{2}} = 10$,
∴ $\frac{1}{2}AB\cdot AC=\frac{1}{2}BC\cdot AG$,
即 $\frac{1}{2}\times8\times6=\frac{1}{2}\times10AG$,
∴ AG = 4.8,
∵ AD 是 BC 边上的中线,
∴ BD = 5,
∴ $S_{\triangle BDF}=S_{\triangle ABD}=\frac{1}{2}\times5\times4.8 = 12$,
即 △BDF 的面积为 12.

解析
(1) 证明:
∵ E 是 AD 的中点,点 F 与点 B 关于点 E 对称,
∴ AE = DE,BE = EF,
∴ 四边形 ABDF 是平行四边形.
(2) △BDF(答案不唯一).
(3) 过点 A 作 AG⊥BC 于点 G,如图所示,
∵ ∠BAC = 90°,AC = 6,AB = 8,
∴ $BC=\sqrt{AB^{2}+AC^{2}}=\sqrt{8^{2}+6^{2}} = 10$,
∴ $\frac{1}{2}AB\cdot AC=\frac{1}{2}BC\cdot AG$,
即 $\frac{1}{2}\times8\times6=\frac{1}{2}\times10AG$,
∴ AG = 4.8,
∵ AD 是 BC 边上的中线,
∴ BD = 5,
∴ $S_{\triangle BDF}=S_{\triangle ABD}=\frac{1}{2}\times5\times4.8 = 12$,
即 △BDF 的面积为 12.

11.几何直观 阅读与思考:
请阅读下列材料,并完成相应的任务.
观察图中的正六边形,点$O$是它的内角平分线的交点,将这个正六边形绕着点$O$旋转$60^{\circ}$,旋转后的图形与旋转前的图形重合.
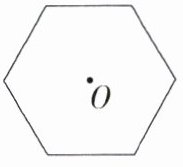
一般地,如果把一个图形绕着某一点旋转一定角度(小于$360^{\circ}$)后,能够与原来的图形重合,那么这个图形叫作旋转对称图形,这个点叫它的对称中心
任务:(M8202003)
(1)中心对称图形______旋转对称图形.(填“是”或“不是”)
(2)下列图形中,不是旋转对称图形的有______,既是旋转对称图形又是中心对称图形的有______,旋转$72^{\circ}$能够完全重合的图形有______.(填字母即可)

请阅读下列材料,并完成相应的任务.
观察图中的正六边形,点$O$是它的内角平分线的交点,将这个正六边形绕着点$O$旋转$60^{\circ}$,旋转后的图形与旋转前的图形重合.

一般地,如果把一个图形绕着某一点旋转一定角度(小于$360^{\circ}$)后,能够与原来的图形重合,那么这个图形叫作旋转对称图形,这个点叫它的对称中心
任务:(M8202003)
(1)中心对称图形______旋转对称图形.(填“是”或“不是”)
(2)下列图形中,不是旋转对称图形的有______,既是旋转对称图形又是中心对称图形的有______,旋转$72^{\circ}$能够完全重合的图形有______.(填字母即可)

答案:
解析
(1) 是.
(2) E;A、C;B、D.
(1) 是.
(2) E;A、C;B、D.
查看更多完整答案,请扫码查看


