《2025年5年中考3年模拟八年级数学下册湘教版》

1.下列图形中，$\triangle A'B'C'$与$\triangle ABC$成中心对称的是（ ）

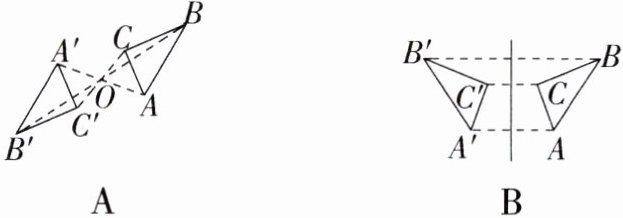
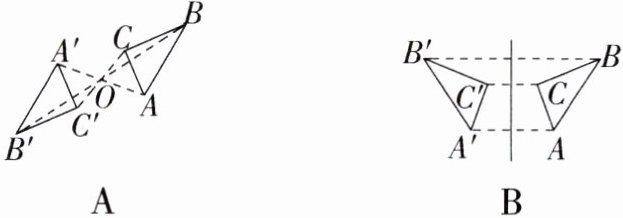
答案： A 由中心对称的定义可知选项 A 符合题意.

2.如图，$\triangle ABO$与$\triangle CDO$关于$O$点成中心对称，点$E,F$在线段$AC$上，且$AF = CE$，下列结论不一定成立的是(M8202003)（ ）

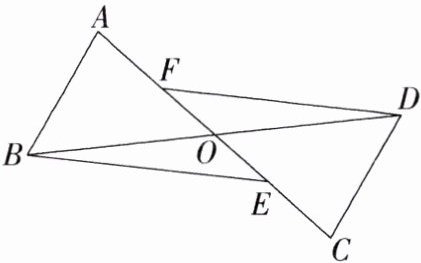
A.$OA = OC$
B.$\angle BAO=\angle CDO$
C.$AB = CD$
D.$FD = BE$

答案： B

∵ △ABO 与 △CDO 关于 O 点成中心对称，
∴ BO = DO，AO = CO，AB = CD，∠BAO = ∠DCO，
∵ AF = CE，
∴ AO - AF = CO - CE，
∴ FO = EO，
在 △FOD 和 △EOB 中，$\begin{cases}FO = EO,\\\angle FOD=\angle EOB,\\DO = BO,\end{cases}$
∴ △FOD≌△EOB(SAS)，
∴ DF = BE.
故选项 A、C、D 中的结论成立，选项 B 中的结论不一定成立. 故选 B.

3.如图，已知$\square ABCD$和直线$MN$，点$O$在直线$MN$上.(M8202003)
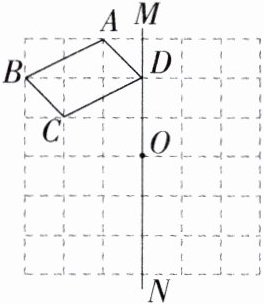
(1)画出$\square A_{1}B_{1}C_{1}D_{1}$，使$\square A_{1}B_{1}C_{1}D_{1}$与$\square ABCD$关于直线$MN$对称.
(2)画出$\square A_{2}B_{2}C_{2}D_{2}$，使$\square A_{2}B_{2}C_{2}D_{2}$与$\square ABCD$关于点$O$成中心对称.
(3)$\square A_{1}B_{1}C_{1}D_{1}$与$\square A_{2}B_{2}C_{2}D_{2}$对称吗？若对称，请在图中画出对称轴或对称中心.

答案：
解析
(1) 如图，□A₁B₁C₁D₁ 即为所求.
(2) 如图，□A₂B₂C₂D₂ 即为所求.
(3) 对称. 如图，□A₁B₁C₁D₁ 与 □A₂B₂C₂D₂ 成轴对称，对称轴为直线 HL.

4.新独家原创 剪纸艺术是最古老的中国民间艺术之一，也是我国非物质文化遗产之一，作为一种镂空艺术，它能给人以视觉上透空的感觉和艺术享受.下列剪纸作品中是中心对称图形的是（ ）

答案： A 根据中心对称图形的定义可知选项 A 符合题意.

5.教材变式·P54T4 如图，$O$是$\square ABCD$的对称中心，$EF$是过点$O$的任意一条直线，它将平行四边形分成两部分，把四边形$ABFE$和四边形$EFCD$的面积分别记为$S_{1},S_{2}$，那么$S_{1},S_{2}$之间的关系为$S_{1}$______$S_{2}$.（填“＞”“=”或“＜”）

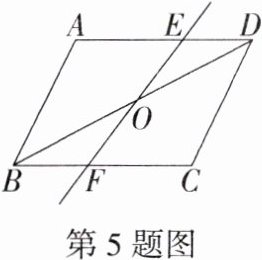
答案： 答案 =
解析
∵ 四边形 ABCD 是平行四边形，
∴ AD//BC，
∴ ∠EDO = ∠FBO，
∵ O 是 □ABCD 的对称中心，
∴ OB = OD，
在 △DEO 与 △BFO 中，$\begin{cases}\angle EDO=\angle FBO,\\OD = OB,\\\angle DOE=\angle BOF,\end{cases}$
∴ △DEO≌△BFO(ASA)，
∴ $S_{\triangle DEO}=S_{\triangle BFO}$，
∵ $S_{\triangle ABD}=S_{\triangle CDB}$，
∴ $S_{四边形AEOB}=S_{四边形CFOD}$，
∵ $S_{1}=S_{四边形AEOB}+S_{\triangle BFO}$，$S_{2}=S_{四边形CFOD}+S_{\triangle DEO}$，
∴ $S_{1}=S_{2}$.

6.数学文化(2024四川自贡中考，7，★☆☆)我国古代数学家赵爽在他所著的《勾股圆方图注》中，运用弦图（如图所示）巧妙地证明了勾股定理.“赵爽弦图”曾作为2002年第24届国际数学家大会的会徽图案.下列关于“赵爽弦图”说法正确的是（ ）

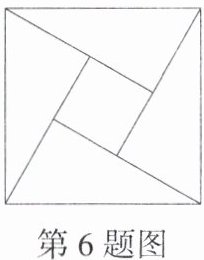
A.是轴对称图形
B.是中心对称图形
C.既是轴对称图形又是中心对称图形
D.既不是轴对称图形也不是中心对称图形

答案： B “赵爽弦图”是中心对称图形，但不是轴对称图形. 故选 B.