第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
8. 求下列函数中自变量x的取值范围.
(1) y = 2x - 3. (2) y = $\frac{1}{x + 1}$. (3) y = $\sqrt{x - 2}$.
(4) y = $\frac{x}{\sqrt{x + 3}}$. (5) y = $\frac{\sqrt{x + 2}}{x - 1}$. (6) y = $\frac{\sqrt{x}}{|x| - 5}$.
(1) y = 2x - 3. (2) y = $\frac{1}{x + 1}$. (3) y = $\sqrt{x - 2}$.
(4) y = $\frac{x}{\sqrt{x + 3}}$. (5) y = $\frac{\sqrt{x + 2}}{x - 1}$. (6) y = $\frac{\sqrt{x}}{|x| - 5}$.
答案:
解析:\n(1)$x$的取值范围为全体实数.\n(2)由题意得$x + 1\neq0$,所以$x\neq - 1$.\n(3)由题意得$x - 2\geqslant0$,所以$x\geqslant2$.\n(4)由题意得$x + 3>0$,所以$x>-3$.\n(5)由题意得$x + 2\geqslant0$且$x - 1\neq0$,所以$x\geqslant - 2$且$x\neq1$.\n(6)由题意得$x\geqslant0$且$\vert x\vert - 5\neq0$,所以$x\geqslant0$且$x\neq5$.
9. 在函数y = 3x + 4中,当x = 1时,函数值为________,当x = ________时,函数值为10.
答案:
答案:$7$;$2$\n解析:当$x = 1$时,$y = 3x + 4 = 3\times1 + 4 = 7$. 当函数值为$10$时,$3x + 4 = 10$,解得$x = 2$.
10. (2024湖南岳阳月考)1~6个月的婴儿生长发育很快,如果一个婴儿出生时的体重为3 300 g,那么他的体重y(g)和月龄x(月)之间的函数关系可以近似用y = 3 300 + 700x来表示,当x的值为3时,y的值为________.(M8204001)
答案:
答案:$5400$\n解析:当$x = 3$时,$y = 3300 + 700x = 3300 + 700\times3 = 3300 + 2100 = 5400$.
11. 已知函数y = |x - 1| + 2.(M8204001)
(1)求自变量等于5时的函数值.
(2)求函数值等于5时的自变量的值.
(1)求自变量等于5时的函数值.
(2)求函数值等于5时的自变量的值.
答案:
解析:\n(1)当$x = 5$时,$y=\vert5 - 1\vert+2 = 4 + 2 = 6$.\n(2)当$y = 5$时,$5=\vert x - 1\vert+2$,解得$x = 4$或$x = - 2$.
12. (2024湖南株洲期末,9,★★☆)根据如图所示的程序计算函数y的值,若输入x的值是1,则输出y的值是-1,若输入x的值是9,则输出y的值是(M8204001) ( )
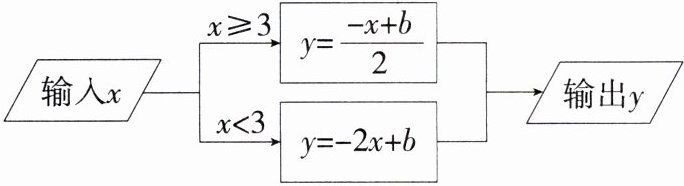
A. 1
B. -17
C. -1
D. -4
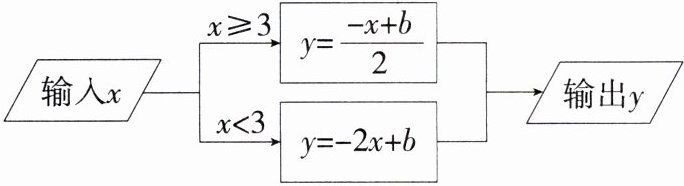
A. 1
B. -17
C. -1
D. -4
答案:
D:由题意可得,当$x = 1$时,$x<3$,代入$y = - 2x + b$得$-1=-2\times1 + b$,$\therefore b = 1$,$\therefore$当输入$x$的值是$9$时,$x>3$,代入$y=\frac{-x + 1}{2}$得$y=\frac{-9 + 1}{2}=-4$,故选 D.
13. 易错题 (2024黑龙江齐齐哈尔中考,13,★★☆)在函数y = $\frac{1}{\sqrt{3 + x}}$ + $\frac{1}{x + 2}$中,自变量x的取值范围是________.(M8204001)
答案:
答案:$x>-3$且$x\neq - 2$\n解析:由题意得$3 + x>0$且$x + 2\neq0$,解得$x>-3$且$x\neq - 2$.
14. 应用意识 (2024河北保定期中)由于惯性,行驶中的汽车在刹车后还要继续向前滑行一段距离才能停止,这段距离称为“刹车距离”.为了测定某小型载客汽车的刹车性能,对这种型号的汽车进行了测试,测得的数据如表.

请回答下列问题:
(1)在这个变化过程中,自变量是________,因变量是________.
(2)当刹车时车速为60 km/h时,刹车距离是________m.
(3)该小型载客汽车在高速公路上发生了一次交通事故,现场测得刹车距离为32 m,推测刹车时车速是多少,并说明事故发生时,小型载客汽车是超速行驶还是正常行驶(相关法规:《中华人民共和国道路交通安全法实施条例》第七十八条:高速公路上行驶的小型载客汽车最高车速不得超过120 km/h)

请回答下列问题:
(1)在这个变化过程中,自变量是________,因变量是________.
(2)当刹车时车速为60 km/h时,刹车距离是________m.
(3)该小型载客汽车在高速公路上发生了一次交通事故,现场测得刹车距离为32 m,推测刹车时车速是多少,并说明事故发生时,小型载客汽车是超速行驶还是正常行驶(相关法规:《中华人民共和国道路交通安全法实施条例》第七十八条:高速公路上行驶的小型载客汽车最高车速不得超过120 km/h)
答案:
解析:\n(1)在这个变化过程中,自变量是刹车时车速,因变量是刹车距离. 故答案为刹车时车速$v$;刹车距离$s$.\n(2)由题表可知,刹车时车速每增加$10\ km/h$,刹车距离增加$2.5\ m$,$12.5 + 2.5 = 15(m)$,$\therefore$当刹车时车速为$60\ km/h$时,刹车距离是$15\ m$. 故答案为$15$.\n(3)由题表可知,刹车时车速每增加$10\ km/h$,刹车距离增加$2.5\ m$,$\therefore$刹车距离$s$与刹车时车速$v$的关系式为$s = 0.25v$. 当$s = 32$时,有$0.25v = 32$,解得$v = 128$,$\because128>120$,$\therefore$刹车时车速是$128\ km/h$,事故发生时,小型载客汽车是超速行驶.
查看更多完整答案,请扫码查看


