《2025年5年中考3年模拟八年级数学下册湘教版》

11.易错题(2024湖南益阳一模,7,★☆☆)如图,两个不同的一次函数$y = ax + b$与$y = bx + a$的图象在同一平面直角坐标系的位置可能是(M8204003) ( )

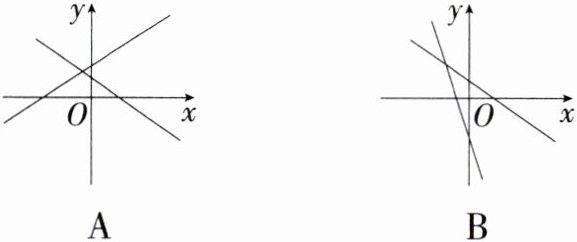
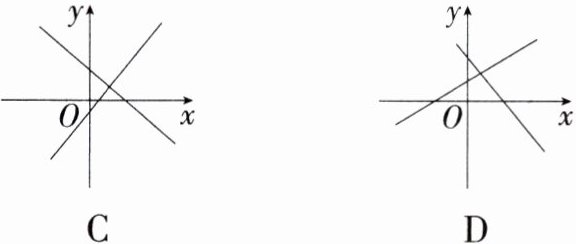
答案： C：\nA. 若经过第一、二、三象限的直线为$y = ax + b$，则$a＞0$，$b＞0$，所以直线$y = bx + a$经过第一、二、三象限，所以 A 选项错误；\nB. 若经过第一、二、四象限的直线为$y = ax + b$，则$a＜0$，$b＞0$，所以直线$y = bx + a$经过第一、三、四象限，所以 B 选项错误；\nC. 若经过第一、三、四象限的直线为$y = ax + b$，则$a＞0$，$b＜0$，所以直线$y = bx + a$经过第一、二、四象限，所以 C 选项正确；\nD. 若经过第一、二、三象限的直线为$y = ax + b$，则$a＞0$，$b＞0$，所以直线$y = bx + a$经过第一、二、三象限，所以 D 选项错误. 故选 C.\n**易错警示**：$k$决定直线$y = kx + b$的倾斜方向，$b$决定直线$y = kx + b$与$y$轴的交点位置，记忆不清易导致错误.

12.(2023山东临沂中考,11,★★☆)对于某个一次函数$y = kx + b(k\neq0)$,根据两位同学的对话得出的结论,错误的是(M8204003) ( )

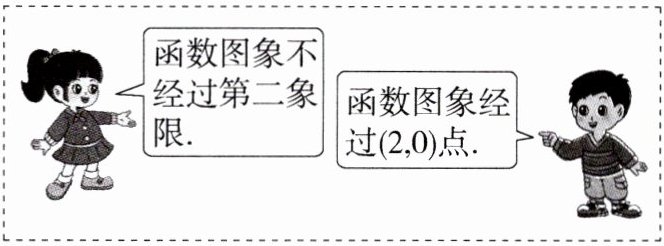
A.$k＞0$
B.$kb＜0$
C.$k + b＞0$
D.$k = -\frac{1}{2}b$

答案： C：$\because$一次函数$y = kx + b(k\neq0)$的图象不经过第二象限，$\therefore k＞0$，$b\leqslant0$，又$\because$函数图象经过点$(2,0)$，$\therefore 2k + b = 0$，即$k=-\frac{1}{2}b$，图象经过第一、三、四象限，$\therefore b＜0$，$\therefore kb＜0$，$k + b=\frac{1}{2}b＜0$，故选 C.

13.[新考法](2022浙江绍兴中考,9,★★☆)已知$(x_1,y_1),(x_2,y_2),(x_3,y_3)$为直线$y = -2x + 3$上的三个点,且$x_1＜x_2＜x_3$,则以下判断正确的是(M8204003) ( )
A.若$x_1x_2＞0$,则$y_1y_3＞0$
B.若$x_1x_3＜0$,则$y_1y_2＞0$
C.若$x_2x_3＞0$,则$y_1y_3＞0$
D.若$x_2x_3＜0$,则$y_1y_2＞0$

答案： D：本题结合一次函数的性质考查函数值的大小，考查形式比较新颖.$\because y=-2x + 3$中，$-2＜0$，$\therefore y$随$x$的增大而减小，当$y = 0$时，$x = 1.5$，$\because(x_{1},y_{1})$，$(x_{2},y_{2})$，$(x_{3},y_{3})$为直线$y=-2x + 3$上的三个点，且$x_{1}＜x_{2}＜x_{3}$.\n若$x_{1}x_{2}＞0$，则$x_{1}$，$x_{2}$同号，但不能确定$y_{1}y_{3}$的正负，故选项 A 不符合题意；\n若$x_{1}x_{3}＜0$，则$x_{1}$，$x_{3}$异号，但不能确定$y_{1}y_{2}$的正负，故选项 B 不符合题意；\n若$x_{2}x_{3}＞0$，则$x_{2}$，$x_{3}$同号，但不能确定$y_{1}y_{3}$的正负，故选项 C 不符合题意；\n若$x_{2}x_{3}＜0$，则$x_{2}$，$x_{3}$异号，即$x_{1}$，$x_{2}$同时为负，$\therefore y_{1}$，$y_{2}$同时为正，$\therefore y_{1}y_{2}＞0$，故选项 D 符合题意. 故选 D.

14.(2024湖南长沙长郡教育集团期中,12,★★☆)一次函数$y = (m - 1)x + m^2$的图象经过点$(0,4)$,且$y$随$x$的增大而增大,则$m =$________.(M8204003)

答案： 答案：$2$\n**解析**：$\because$一次函数$y=(m - 1)x+m^{2}$的图象经过点$(0,4)$，且$y$随$x$的增大而增大，$\therefore m - 1＞0$且$m^{2}=4$，$\therefore m = 2$.

15.(2023天津中考,16,★☆☆)若直线$y = x$向上平移3个单位长度后经过点$(2,m)$,则$m$的值为__________.(M8204003)

答案： 答案：$5$\n**解析**：将直线$y = x$向上平移$3$个单位长度，得到直线$y = x + 3$，把点$(2,m)$的坐标代入，得$m = 2 + 3 = 5$.

16.(2023重庆中考A卷,23,★★☆)如图,$\triangle ABC$是边长为4的等边三角形,动点$E,F$分别以每秒1个单位长度的速度同时从点$A$出发,点$E$沿折线$A→B→C$方向运动,点$F$沿折线$A→C→B$方向运动,当两者相遇时停止运动.设运动时间为$t$秒,点$E,F$的距离为$y$.(M8204003)
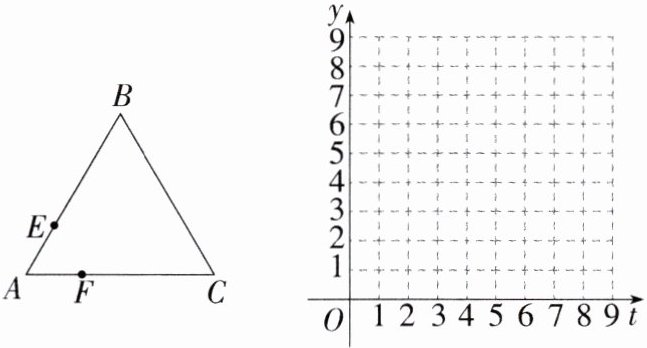
(1)请直接写出$y$关于$t$的函数表达式并注明自变量$t$的取值范围.
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质.
(3)结合函数图象,写出点$E,F$相距3个单位长度时$t$的值.
                                                           

答案：
解析：
(1)$y=\begin{cases}t(0\leqslant t\leqslant4)\\12 - 2t(4＜t\leqslant6)\end{cases}$.
(2)函数图象如图.

根据函数图象可知，函数的性质为（写出其中一条即可）：\n①当$0\leqslant t\leqslant4$时，$y$随$t$的增大而增大；当$4＜t\leqslant6$时，$y$随$t$的增大而减小.\n②该函数在自变量的取值范围内，有最大值和最小值，当$t = 4$时，函数取得最大值，为$4$；当$t = 0$或$t = 6$时，函数取得最小值，为$0$.\n
(3)当$t = 3$或$t = 4.5$时，点$E$，$F$相距$3$个单位长度. 提示：结合图象和
(1)中所求表达式可知，当$0\leqslant t\leqslant4$时，若$y = 3$，则$t = 3$；当$4＜t\leqslant6$时，若$y = 3$，则$t = 4.5$.