《2025年5年中考3年模拟八年级数学下册湘教版》

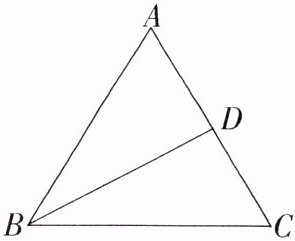
20.[答案含评分细则](2023湖南长沙岳麓长郡梅溪湖中学月考)(10分)如图,△ABC中,AB = AC,BC = 10,D是AC上一点,且CD = 6,BD = 8.
(1)求证:△BDC是直角三角形.
(2)求AB的长.

答案： 解析：\n（1）证明：$\because BC = 10$，$CD = 6$，$BD = 8$，$\therefore BC^{2}=CD^{2}+BD^{2}$，$\cdots\cdots3$分\n$\therefore\triangle BDC$是直角三角形，$\angle BDC = 90^{\circ}$。$\cdots\cdots5$分\n（2）设$AB = AC = x$，则$AD = x - 6$，$\cdots\cdots6$分\n$\because\angle ADB=\angle BDC = 90^{\circ}$，$\therefore AB^{2}=AD^{2}+BD^{2}$，$\therefore x^{2}=(x - 6)^{2}+8^{2}$，$\cdots\cdots8$分\n解得$x=\frac{25}{3}$，故$AB=\frac{25}{3}$。$\cdots\cdots10$分

21.[答案含评分细则](10分)如图,在由边长为1的小正方形组成的5×6的网格中,△ABC的三个顶点均在格点上,请按要求解答下列问题:
(1)通过计算判断△ABC的形状.
(2)在该网格中确定一个格点D,连接AD,CD,使四边形ABCD为平行四边形,并求出□ABCD的面积.

答案：
解析：\n（1）由题意可得$AB=\sqrt{1^{2}+2^{2}}=\sqrt{5}$，$AC=\sqrt{2^{2}+4^{2}}=2\sqrt{5}$，$BC=\sqrt{3^{2}+4^{2}}=5$，$\cdots\cdots3$分\n$\because(\sqrt{5})^{2}+(2\sqrt{5})^{2}=25 = 5^{2}$，$\therefore AB^{2}+AC^{2}=BC^{2}$，$\therefore\triangle ABC$是直角三角形，$\angle BAC = 90^{\circ}$。$\cdots\cdots5$分\n（2）如图，过点$A$作$AD// BC$，过点$C$作$CD// AB$，直线$AD$和$CD$的交点就是格点$D$的位置。$\cdots\cdots8$分\n$\therefore S_{\square ABCD}=AB\cdot AC=\sqrt{5}\times2\sqrt{5}=10$。$\cdots\cdots10$分

22.[答案含评分细则](2023湖南衡阳咸水中学一模)(12分)如图,在△ABC中,AB = AC,AD是BC边上的高,AE//BC,BC = 2AE.
(1)求证:四边形ADCE是矩形.
(2)F是AB的中点,连接DF,EF,若∠DFE = 90°,AB = 4,求EF的长.

答案：
解析：\n（1）证明：$\because AB = AC$，$AD$是$BC$边上的高，$\therefore BC = 2BD = 2DC$，$\angle ADC = 90^{\circ}$，$\cdots\cdots2$分\n$\because BC = 2AE$，$\therefore AE = DC$，又$\because AE// BC$，$\therefore$四边形$AECD$为平行四边形，$\cdots\cdots4$分\n$\because\angle ADC = 90^{\circ}$，$\therefore$平行四边形$ADCE$是矩形。$\cdots\cdots6$分\n（2）如图，连接$DE$，$\cdots\cdots7$分\n$\because F$是$AB$的中点，$AD\perp BC$，$AB = 4$，$\therefore DF=\frac{1}{2}AB = 2$，$\cdots9$分\n$\because$四边形$ADCE$是矩形，$\therefore DE = AC = AB = 4$，$\because\angle DFE = 90^{\circ}$，$\therefore EF=\sqrt{DE^{2}-DF^{2}}=\sqrt{4^{2}-2^{2}}=2\sqrt{3}$。$\cdots\cdots12$分

23.[答案含评分细则](2024北京二中教育集团一模)(12分)如图,在等腰△ABC中,AB = BC,BO平分∠ABC,过点A作AD//BC交BO的延长线于点D,连接CD,过点D作DE⊥BD交BC的延长线于点E.
(1)判断四边形ABCD的形状,并说明理由.
(2)若AB = 4,∠ABE = 120°,求DE的长.

答案： 解析：\n（1）四边形$ABCD$是菱形，$\cdots\cdots1$分\n理由：$\because AB = BC$，$BO$平分$\angle ABC$，$\therefore AO = CO$，$\because AD// BE$，$\therefore\angle DAO=\angle ACB$，$\angle ADO=\angle CBO$，$\therefore\triangle ADO\cong\triangle CBO(AAS)$，$\therefore DO = BO$，$\cdots\cdots4$分\n$\therefore$四边形$ABCD$是平行四边形，$\because AB = BC$，$\therefore$四边形$ABCD$是菱形。$\cdots\cdots6$分\n（2）$\because$四边形$ABCD$是菱形，$\therefore BC = AB = 4$，$\because BO$平分$\angle ABC$，$\angle ABE = 120^{\circ}$，$\therefore\angle DBC=\frac{1}{2}\angle ABE = 60^{\circ}$，$\cdots\cdots7$分\n$\because BC = CD$，$\therefore\triangle BCD$是等边三角形，$\therefore BD = BC = 4$，$\cdots\cdots9$分\n$\because BD\perp DE$，$\therefore\angle BDE = 90^{\circ}$，$\therefore\angle E = 90^{\circ}-\angle DBC = 30^{\circ}$，$\therefore BE = 2BD = 8$，$\therefore DE=\sqrt{BE^{2}-BD^{2}}=\sqrt{8^{2}-4^{2}}=4\sqrt{3}$。$\cdots\cdots12$分

24.[答案含评分细则](14分)如图1,四边形ABCD是正方形,点E、K分别在BC、AB上,点G在BA的延长线上,且CE = BK = AG,连接DE、CK、DG.(M8202005)
(1)求证:①DE = DG;②DE⊥DG.
(2)以线段DE、DG为边作出正方形DEFG,连接KF,如图2,猜想四边形CEFK是怎样的特殊四边形,并证明你的猜想.

答案：
解析：\n（1）①证明：$\because$四边形$ABCD$是正方形，$\therefore AD = DC$，$\angle GAD=\angle DCE = 90^{\circ}$，在$\triangle GAD$和$\triangle ECD$中，$\begin{cases}AG = CE\\\angle GAD=\angle ECD\\AD = CD\end{cases}$，$\therefore\triangle GAD\cong\triangle ECD(SAS)$，$\therefore DE = DG$。$\cdots\cdots4$分\n②证明：$\because$四边形$ABCD$是正方形，$\therefore\angle ADC = 90^{\circ}$，$\because\triangle GAD\cong\triangle ECD$，$\therefore\angle GDA=\angle CDE$，$\therefore\angle GDE=\angle GDA+\angle ADE=\angle CDE+\angle ADE=\angle ADC = 90^{\circ}$，$\therefore DE\perp DG$。$\cdots\cdots7$分\n（2）四边形$CEFK$是平行四边形。$\cdots\cdots8$分\n证明：设$CK$与$DE$交于点$O$，如图，$\because$四边形$ABCD$是正方形，$\therefore\angle B=\angle ECD = 90^{\circ}$，$BC = CD$，在$\triangle KBC$和$\triangle ECD$中，$\begin{cases}BC = CD\\\angle B=\angle ECD\\KB = EC\end{cases}$，$\therefore\triangle KBC\cong\triangle ECD(SAS)$，$\therefore DE = CK$，$\angle DEC=\angle BKC$，$\cdots\cdots10$分\n$\because\angle B = 90^{\circ}$，$\therefore\angle KCB+\angle BKC = 90^{\circ}$，$\therefore\angle KCB+\angle DEC = 90^{\circ}$，$\therefore\angle EOC = 180^{\circ}-90^{\circ}=90^{\circ}$，$\cdots\cdots12$分\n$\because$四边形$DEFG$是正方形，$\therefore DE = EF = CK$，$\angle FED = 90^{\circ}=\angle EOC$，$\therefore CK// EF$，$\therefore$四边形$CEFK$是平行四边形。$\cdots\cdots14$分