第36页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
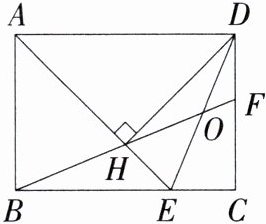
8.(2024湖南益阳二模,10,★★☆)如图,在矩形ABCD中,$ AD = \sqrt{2}AB $,$ \angle BAD $的平分线AE交BC于点E,$ DH \perp AE $于点H,连接BH并延长交CD于点F,连接DE交BF于点O,有下列结论:①ED平分$ \angle AEC $;②$ OE = \frac{1}{2}DE $;③$ HE = DF $;④$ AB = FH $.其中正确的结论有 ( )
A.4个
B.3个
C.2个
D.1个

A.4个
B.3个
C.2个
D.1个
答案:
B
∵ 在矩形 $ABCD$ 中,$\angle BAD = 90^{\circ}$,$AE$ 平分 $\angle BAD$,
∴ $\angle BAE=\angle DAE = 45^{\circ}$,
∴ $\triangle ABE$ 是等腰直角三角形,
∴ $AE=\sqrt{2}AB$,
∵ $AD=\sqrt{2}AB$,
∴ $AE = AD$,
∴ $\angle AED=\angle ADE$,
∵ $AD// BC$,
∴ $\angle ADE=\angle CED$,
∴ $\angle AED=\angle CED$,
∴ $ED$ 平分 $\angle AEC$,故结论①正确;\n
∵ $\angle BAE=\angle DAE = 45^{\circ}$,
∴ $\triangle ADH$ 是等腰直角三角形,
∴ $AD=\sqrt{2}AH=\sqrt{2}AB$,
∴ $AH = AB$,
∴ $\angle ABH=\angle AHB=\frac{1}{2}\times(180^{\circ}-45^{\circ}) = 67.5^{\circ}=\angle OHE$,由结论①得 $\angle AED=\frac{1}{2}\times(180^{\circ}-45^{\circ})=\angle CED = 67.5^{\circ}$,
∴ $\angle OHE=\angle AED$,
∴ $OE = OH$,
∵ $\angle OHD = 90^{\circ}-67.5^{\circ}=22.5^{\circ}$,$\angle ODH = 90^{\circ}-67.5^{\circ}=22.5^{\circ}$,
∴ $\angle OHD=\angle ODH$,
∴ $OH = OD$,
∴ $OE = OD = OH$,$OE=\frac{1}{2}DE$,故结论②正确;\n
∵ $\angle EBH = 90^{\circ}-67.5^{\circ}=22.5^{\circ}$,
∴ $\angle EBH=\angle DHF$,又
∵ $BE = AB = AH = DH$,$\angle HEB=\angle FDH = 45^{\circ}$,
∴ $\triangle BEH\cong\triangle HDF(ASA)$,
∴ $BH = FH$,$HE = DF$,故结论③正确;\n
∵ $AB = AH$,$\angle BAE = 45^{\circ}$,
∴ $\triangle ABH$ 不是等边三角形,
∴ $AB\neq BH$,
∴ $AB\neq FH$,故结论④错误. 综上,正确的结论有 3 个,故选 B.
∵ 在矩形 $ABCD$ 中,$\angle BAD = 90^{\circ}$,$AE$ 平分 $\angle BAD$,
∴ $\angle BAE=\angle DAE = 45^{\circ}$,
∴ $\triangle ABE$ 是等腰直角三角形,
∴ $AE=\sqrt{2}AB$,
∵ $AD=\sqrt{2}AB$,
∴ $AE = AD$,
∴ $\angle AED=\angle ADE$,
∵ $AD// BC$,
∴ $\angle ADE=\angle CED$,
∴ $\angle AED=\angle CED$,
∴ $ED$ 平分 $\angle AEC$,故结论①正确;\n
∵ $\angle BAE=\angle DAE = 45^{\circ}$,
∴ $\triangle ADH$ 是等腰直角三角形,
∴ $AD=\sqrt{2}AH=\sqrt{2}AB$,
∴ $AH = AB$,
∴ $\angle ABH=\angle AHB=\frac{1}{2}\times(180^{\circ}-45^{\circ}) = 67.5^{\circ}=\angle OHE$,由结论①得 $\angle AED=\frac{1}{2}\times(180^{\circ}-45^{\circ})=\angle CED = 67.5^{\circ}$,
∴ $\angle OHE=\angle AED$,
∴ $OE = OH$,
∵ $\angle OHD = 90^{\circ}-67.5^{\circ}=22.5^{\circ}$,$\angle ODH = 90^{\circ}-67.5^{\circ}=22.5^{\circ}$,
∴ $\angle OHD=\angle ODH$,
∴ $OH = OD$,
∴ $OE = OD = OH$,$OE=\frac{1}{2}DE$,故结论②正确;\n
∵ $\angle EBH = 90^{\circ}-67.5^{\circ}=22.5^{\circ}$,
∴ $\angle EBH=\angle DHF$,又
∵ $BE = AB = AH = DH$,$\angle HEB=\angle FDH = 45^{\circ}$,
∴ $\triangle BEH\cong\triangle HDF(ASA)$,
∴ $BH = FH$,$HE = DF$,故结论③正确;\n
∵ $AB = AH$,$\angle BAE = 45^{\circ}$,
∴ $\triangle ABH$ 不是等边三角形,
∴ $AB\neq BH$,
∴ $AB\neq FH$,故结论④错误. 综上,正确的结论有 3 个,故选 B.
9.(2024湖南永州东安期中,17,★★☆)如图所示,矩形ABCD的对角线AC和BD相交于点O,过点O的直线分别交AD、BC于点E、F,$ AB = 2 $,$ BC = 3 $,则图中阴影部分的面积为______.


答案:
答案 $3$\n**解析**
∵ 四边形 $ABCD$ 是矩形,
∴ $OA = OC$,$AD// BC$,
∴ $\angle AEO=\angle CFO$,
∵ $\angle AOE=\angle COF$,
∴ $\triangle AOE\cong\triangle COF$,则 $S_{\triangle AOE}=S_{\triangle COF}$,
∴ $S_{阴影}=S_{\triangle AOE}+S_{\triangle BOF}+S_{\triangle COD}=S_{\triangle COF}+S_{\triangle BOF}+S_{\triangle COD}=S_{\triangle BCD}$,
∵ $S_{\triangle BCD}=\frac{1}{2}CD\cdot BC=\frac{1}{2}\times3\times2 = 3$,
∴ $S_{阴影}=3$.
∵ 四边形 $ABCD$ 是矩形,
∴ $OA = OC$,$AD// BC$,
∴ $\angle AEO=\angle CFO$,
∵ $\angle AOE=\angle COF$,
∴ $\triangle AOE\cong\triangle COF$,则 $S_{\triangle AOE}=S_{\triangle COF}$,
∴ $S_{阴影}=S_{\triangle AOE}+S_{\triangle BOF}+S_{\triangle COD}=S_{\triangle COF}+S_{\triangle BOF}+S_{\triangle COD}=S_{\triangle BCD}$,
∵ $S_{\triangle BCD}=\frac{1}{2}CD\cdot BC=\frac{1}{2}\times3\times2 = 3$,
∴ $S_{阴影}=3$.
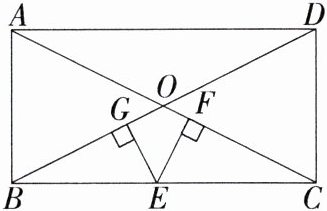
10. [情境题·中华优秀传统文化](2023四川内江中考,16,★★☆)出入相补原理是我国古代数学的重要成就之一,最早是由数学家刘徽创建的.“将一个几何图形,任意切成多个小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形ABCD中,$ AB = 5 $,$ AD = 12 $,对角线AC与BD交于点O,点E为BC边上的一个动点,$ EF \perp AC $,$ EG \perp BD $,垂足分别为F,G,则$ EF + EG = $______.

答案:
答案 $\frac{60}{13}$\n**解析** 如图,连接 $OE$,
∵ 四边形 $ABCD$ 是矩形,
∴ $\angle ABC = 90^{\circ}$,$BC = AD = 12$,$AO = CO = BO = DO$,
∵ $AB = 5$,
∴ $AC=\sqrt{AB^{2}+BC^{2}} = 13$,
∴ $OB = OC=\frac{13}{2}$,
∵ $S_{\triangle BOE}+S_{\triangle COE}=S_{\triangle BOC}$,
∴ $\frac{1}{2}OB\cdot EG+\frac{1}{2}OC\cdot EF=\frac{1}{2}\times\frac{1}{2}\times5\times12$,
∴ $\frac{1}{2}\times\frac{13}{2}EG+\frac{1}{2}\times\frac{13}{2}EF=\frac{1}{2}\times\frac{13}{2}(EG + EF)=15$,
∴ $EG + EF=\frac{60}{13}$.

答案 $\frac{60}{13}$\n**解析** 如图,连接 $OE$,
∵ 四边形 $ABCD$ 是矩形,
∴ $\angle ABC = 90^{\circ}$,$BC = AD = 12$,$AO = CO = BO = DO$,
∵ $AB = 5$,
∴ $AC=\sqrt{AB^{2}+BC^{2}} = 13$,
∴ $OB = OC=\frac{13}{2}$,
∵ $S_{\triangle BOE}+S_{\triangle COE}=S_{\triangle BOC}$,
∴ $\frac{1}{2}OB\cdot EG+\frac{1}{2}OC\cdot EF=\frac{1}{2}\times\frac{1}{2}\times5\times12$,
∴ $\frac{1}{2}\times\frac{13}{2}EG+\frac{1}{2}\times\frac{13}{2}EF=\frac{1}{2}\times\frac{13}{2}(EG + EF)=15$,
∴ $EG + EF=\frac{60}{13}$.

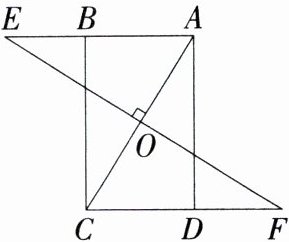
11.(2024贵州遵义汇川一模,21,★★☆)在矩形ABCD中,过对角线AC的中点O作$ EF \perp AC $,分别与AB和CD的延长线交于点E,F.
(1)求证:$ \triangle AOE \cong \triangle COF $.
(2)若$ AB = 6 $,$ AD = 8 $,求AC与EF的长.
(1)求证:$ \triangle AOE \cong \triangle COF $.
(2)若$ AB = 6 $,$ AD = 8 $,求AC与EF的长.

答案:
解析 \n(1)**证明**:
∵ 四边形 $ABCD$ 是矩形,
∴ $AB// CD$,
∴ $\angle E=\angle F$,
∵ 点 $O$ 是 $AC$ 的中点,
∴ $AO = CO$,在 $\triangle AOE$ 和 $\triangle COF$ 中,$\begin{cases}\angle E=\angle F\\\angle AOE=\angle COF\\AO = CO\end{cases}$,
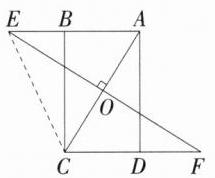
∴ $\triangle AOE\cong\triangle COF(AAS)$.\n(2)如图,连接 $CE$,由(1)得 $\triangle AOE\cong\triangle COF$,
∴ $OE = OF$,$BE = AE - AB = CF - CD = DF$,
∵ $OE = OF$,$AC\perp EF$,
∴ $AC$ 垂直平分 $EF$,
∴ $CE = CF=\sqrt{BC^{2}+BE^{2}}=\sqrt{8^{2}+(CF - 6)^{2}}$,
∴ $AE = CF=\frac{25}{3}$,
∵ $AC=\sqrt{AB^{2}+BC^{2}} = 10$,
∴ $AO = CO=\frac{1}{2}AC = 5$,
∵ $OE=\sqrt{AE^{2}-AO^{2}}=\sqrt{(\frac{25}{3})^{2}-5^{2}}=\frac{20}{3}$,
∴ $EF=\frac{40}{3}$.
∴ $AC = 10$,$EF=\frac{40}{3}$.
解析 \n(1)**证明**:
∵ 四边形 $ABCD$ 是矩形,
∴ $AB// CD$,
∴ $\angle E=\angle F$,
∵ 点 $O$ 是 $AC$ 的中点,
∴ $AO = CO$,在 $\triangle AOE$ 和 $\triangle COF$ 中,$\begin{cases}\angle E=\angle F\\\angle AOE=\angle COF\\AO = CO\end{cases}$,
∴ $\triangle AOE\cong\triangle COF(AAS)$.\n(2)如图,连接 $CE$,由(1)得 $\triangle AOE\cong\triangle COF$,
∴ $OE = OF$,$BE = AE - AB = CF - CD = DF$,
∵ $OE = OF$,$AC\perp EF$,
∴ $AC$ 垂直平分 $EF$,
∴ $CE = CF=\sqrt{BC^{2}+BE^{2}}=\sqrt{8^{2}+(CF - 6)^{2}}$,
∴ $AE = CF=\frac{25}{3}$,
∵ $AC=\sqrt{AB^{2}+BC^{2}} = 10$,
∴ $AO = CO=\frac{1}{2}AC = 5$,
∵ $OE=\sqrt{AE^{2}-AO^{2}}=\sqrt{(\frac{25}{3})^{2}-5^{2}}=\frac{20}{3}$,
∴ $EF=\frac{40}{3}$.
∴ $AC = 10$,$EF=\frac{40}{3}$.

12. [推理能力](1)探究规律:如图1,点P为平行四边形ABCD内一点,$ \triangle PAB $、$ \triangle PCD $的面积分别记为$ S_{1} $、$ S_{2} $,平行四边形ABCD的面积记为S,试探究$ S_{1} + S_{2} $与S之间的关系.
(2)解决问题:如图2,矩形ABCD中,$ AB = 5 $,$ BC = 8 $,点E、F、G、H分别在AB、BC、CD、DA上,且$ AE = CG = 3 $,$ AH = CF = 2 $,连接EG、HF交于点P,四边形AEPH、四边形CGPF的面积分别记为$ S_{1} $、$ S_{2} $,求$ S_{1} + S_{2} $的值.
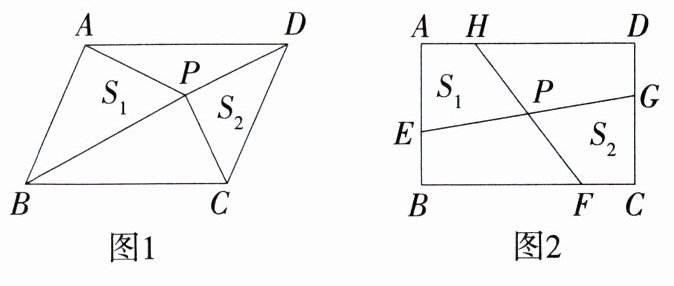
(2)解决问题:如图2,矩形ABCD中,$ AB = 5 $,$ BC = 8 $,点E、F、G、H分别在AB、BC、CD、DA上,且$ AE = CG = 3 $,$ AH = CF = 2 $,连接EG、HF交于点P,四边形AEPH、四边形CGPF的面积分别记为$ S_{1} $、$ S_{2} $,求$ S_{1} + S_{2} $的值.

答案:
解析 \n(1)如图①所示,过点 $P$ 作 $PG\perp BA$ 交 $BA$ 于点 $G$,延长 $GP$ 交 $CD$ 于点 $H$,
∵ 四边形 $ABCD$ 是平行四边形,
∴ $AB// CD$,$AB = CD$,
∵ $PG\perp AB$,
∴ $PH\perp CD$,
∴ $S_{1}=\frac{1}{2}AB\cdot PG$,$S_{2}=\frac{1}{2}CD\cdot PH$,
∴ $S_{1}+S_{2}=\frac{1}{2}AB\cdot PG+\frac{1}{2}CD\cdot PH=\frac{1}{2}AB\cdot PG+\frac{1}{2}AB\cdot PH=\frac{1}{2}AB\cdot(PG + PH)=\frac{1}{2}AB\cdot GH=\frac{1}{2}S$.\n(2)如图②所示,过点 $P$ 作 $PK\perp AB$ 于点 $K$,并延长 $KP$ 交 $CD$ 于点 $T$,过点 $P$ 作 $PM\perp AD$ 于点 $M$,并延长 $MP$ 交 $BC$ 于点 $N$,连接 $PA$,$PB$,$PC$,$PD$,
∵ 四边形 $ABCD$ 是矩形,
∴ $AD// BC$,$AB// CD$,
∵ $KT\perp AB$,$MN\perp AD$,
∴ $KT\perp CD$,$MN\perp BC$,
∴ $PK + PT = BC = 8$,$PM+PN = AB = 5$,
∴ $S_{1}+S_{2}=\frac{1}{2}AE\cdot PK+\frac{1}{2}AH\cdot PM+\frac{1}{2}CG\cdot PT+\frac{1}{2}CF\cdot PN=\frac{1}{2}\times3PK+\frac{1}{2}\times2PM+\frac{1}{2}\times3PT+\frac{1}{2}\times2PN=\frac{3}{2}PK+PM+\frac{3}{2}PT+PN=\frac{3}{2}BC+AB = 12 + 5 = 17$.

解析 \n(1)如图①所示,过点 $P$ 作 $PG\perp BA$ 交 $BA$ 于点 $G$,延长 $GP$ 交 $CD$ 于点 $H$,
∵ 四边形 $ABCD$ 是平行四边形,
∴ $AB// CD$,$AB = CD$,
∵ $PG\perp AB$,
∴ $PH\perp CD$,
∴ $S_{1}=\frac{1}{2}AB\cdot PG$,$S_{2}=\frac{1}{2}CD\cdot PH$,
∴ $S_{1}+S_{2}=\frac{1}{2}AB\cdot PG+\frac{1}{2}CD\cdot PH=\frac{1}{2}AB\cdot PG+\frac{1}{2}AB\cdot PH=\frac{1}{2}AB\cdot(PG + PH)=\frac{1}{2}AB\cdot GH=\frac{1}{2}S$.\n(2)如图②所示,过点 $P$ 作 $PK\perp AB$ 于点 $K$,并延长 $KP$ 交 $CD$ 于点 $T$,过点 $P$ 作 $PM\perp AD$ 于点 $M$,并延长 $MP$ 交 $BC$ 于点 $N$,连接 $PA$,$PB$,$PC$,$PD$,
∵ 四边形 $ABCD$ 是矩形,
∴ $AD// BC$,$AB// CD$,
∵ $KT\perp AB$,$MN\perp AD$,
∴ $KT\perp CD$,$MN\perp BC$,
∴ $PK + PT = BC = 8$,$PM+PN = AB = 5$,
∴ $S_{1}+S_{2}=\frac{1}{2}AE\cdot PK+\frac{1}{2}AH\cdot PM+\frac{1}{2}CG\cdot PT+\frac{1}{2}CF\cdot PN=\frac{1}{2}\times3PK+\frac{1}{2}\times2PM+\frac{1}{2}\times3PT+\frac{1}{2}\times2PN=\frac{3}{2}PK+PM+\frac{3}{2}PT+PN=\frac{3}{2}BC+AB = 12 + 5 = 17$.

查看更多完整答案,请扫码查看


