第61页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
7.(2024贵州中考,6,★☆☆)为培养青少年的科学态度和科学思维,某校创建了“科技创新”社团.小红将“科”“技”“创”“新”写在如图所示的方格纸中,若建立平面直角坐标系,使“创”“新”对应的点的坐标分别为(-2,0),(0,0),则“技”对应的点所在的象限为 ( )

A.第一象限
B.第二象限
C.第三象限
D.第四象限

A.第一象限
B.第二象限
C.第三象限
D.第四象限
答案:
A 根据题意建立直角坐标系如图, 可知 “技” 在第一象限, 故选 A.
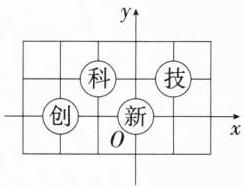
A 根据题意建立直角坐标系如图, 可知 “技” 在第一象限, 故选 A.

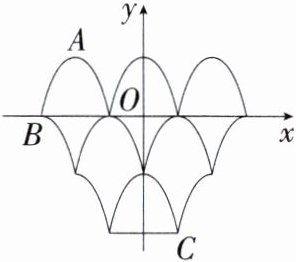
8.情境题·中华优秀传统文化 (2024湖南株洲模拟,14,★☆☆)窗格是中国传统建筑装饰的重要构成元素,是中国传统建筑文化的重要组成部分.下图是部分窗格的截面示意图,将其放置在平面直角坐标系中,点A,B,C均为曲线的端点,若点A的坐标为(-2,√3),点B的坐标为(-3,0),则点C的坐标为________.

答案:
答案 $(1,-2\sqrt{3})$
解析 由题图知, 点 $C$ 在第四象限, $\because A$ 点的纵坐标为$\sqrt{3}$, $\therefore C$ 点的纵坐标为$-2\sqrt{3}$, $\because A,B$ 的横坐标分别为$-2,-3$, $\therefore C$ 点的横坐标为 $1$, $\therefore$ 点 $C$ 的坐标为$(1,-2\sqrt{3})$.
解析 由题图知, 点 $C$ 在第四象限, $\because A$ 点的纵坐标为$\sqrt{3}$, $\therefore C$ 点的纵坐标为$-2\sqrt{3}$, $\because A,B$ 的横坐标分别为$-2,-3$, $\therefore C$ 点的横坐标为 $1$, $\therefore$ 点 $C$ 的坐标为$(1,-2\sqrt{3})$.
9.跨艺术·棋盘类 (2024广西柳州模拟,23,★★☆)如图所示的是中国象棋棋盘的一部分,棋子“马”走的规则是沿“日”字形的对角线走.例如:图中“马”所在的位置可以直接走到点A或点B处.
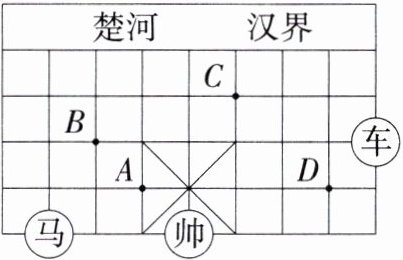
(1)如果“帅”位于点(0,0),“车”位于点(4,2),则“马”所在的点的坐标为________,点C的坐标为________,点D的坐标为________.
(2)在(1)的条件下,若“马”的位置在C点,为了到达D点,请按“马”走的规则,写出一种你认为合理的行走路线,并用坐标表示.

(1)如果“帅”位于点(0,0),“车”位于点(4,2),则“马”所在的点的坐标为________,点C的坐标为________,点D的坐标为________.
(2)在(1)的条件下,若“马”的位置在C点,为了到达D点,请按“马”走的规则,写出一种你认为合理的行走路线,并用坐标表示.
答案:
解析
(1) 根据题意画出平面直角坐标系如图, 则 “马” 所在的点的坐标为$(-3,0)$, 点 $C$ 的坐标为$(1,3)$, 点 $D$ 的坐标为$(3,1)$. 故答案为$(-3,0);(1,3);(3,1)$.
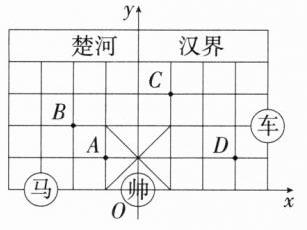
(2) 若 “马” 的位置在 $C$ 点, 为了到达 $D$ 点, 则所走路线可以为 $C(1,3)\to(2,1)\to(3,3)\to(1,2)\to D(3,1)$ (答案不唯一).
解析
(1) 根据题意画出平面直角坐标系如图, 则 “马” 所在的点的坐标为$(-3,0)$, 点 $C$ 的坐标为$(1,3)$, 点 $D$ 的坐标为$(3,1)$. 故答案为$(-3,0);(1,3);(3,1)$.

(2) 若 “马” 的位置在 $C$ 点, 为了到达 $D$ 点, 则所走路线可以为 $C(1,3)\to(2,1)\to(3,3)\to(1,2)\to D(3,1)$ (答案不唯一).
10.新考向·新定义试题 抽象能力 在平面直角坐标系xOy中,对于点P(x,y),若点Q的坐标为(kx + y,x + ky),其中k为常数,则称点Q是点P的“k级关联点”.例如,点P(1,4)的“3级关联点”为Q(3×1 + 4,1 + 3×4),即Q(7,13).
(1)已知点A(2,-6)的“1/2级关联点”是B,求点B的坐标.
(2)已知点C的“5级关联点”的坐标为(9,-3),求点C的坐标.
(3)已知点M(m - 1,2m)的“-4级关联点”N在坐标轴上,求点N的坐标.
(1)已知点A(2,-6)的“1/2级关联点”是B,求点B的坐标.
(2)已知点C的“5级关联点”的坐标为(9,-3),求点C的坐标.
(3)已知点M(m - 1,2m)的“-4级关联点”N在坐标轴上,求点N的坐标.
答案:
解析
(1) $\because$ 点 $A(2,-6)$ 的 “$\frac{1}{2}$ 级关联点” 是 $B$,
$\therefore$ 点 $B$ 的坐标为$(\frac{1}{2}\times2 - 6,2-\frac{1}{2}\times6)$,
即点 $B$ 的坐标为$(-5,-1)$.
(2) 设点 $C$ 的坐标为$(a,b)$,
$\because$ 点 $C$ 的 “$5$ 级关联点” 为$(9,-3)$,
$\therefore\begin{cases}5a + b = 9,\\a + 5b = -3,\end{cases}$ 解得$\begin{cases}a = 2,\\b = -1,\end{cases}$ $\therefore$ 点 $C$ 的坐标为$(2,-1)$.
(3) 由题意知点 $M(m - 1,2m)$ 的 “$-4$ 级关联点” 为 $N(-4(m - 1)+2m,m - 1+(-4)\times2m)$,
当点 $N$ 在 $y$ 轴上时, $-4(m - 1)+2m = 0$, 解得 $m = 2$,
$\therefore m - 1+(-4)\times2m = -15$, $\therefore N(0,-15)$;
当点 $N$ 在 $x$ 轴上时, $m - 1+(-4)\times2m = 0$,
解得 $m = -\frac{1}{7}$, $\therefore -4(m - 1)+2m = \frac{30}{7}$, $\therefore N(\frac{30}{7},0)$.
综上所述, 点 $N$ 的坐标为$(0,-15)$ 或$(\frac{30}{7},0)$.
(1) $\because$ 点 $A(2,-6)$ 的 “$\frac{1}{2}$ 级关联点” 是 $B$,
$\therefore$ 点 $B$ 的坐标为$(\frac{1}{2}\times2 - 6,2-\frac{1}{2}\times6)$,
即点 $B$ 的坐标为$(-5,-1)$.
(2) 设点 $C$ 的坐标为$(a,b)$,
$\because$ 点 $C$ 的 “$5$ 级关联点” 为$(9,-3)$,
$\therefore\begin{cases}5a + b = 9,\\a + 5b = -3,\end{cases}$ 解得$\begin{cases}a = 2,\\b = -1,\end{cases}$ $\therefore$ 点 $C$ 的坐标为$(2,-1)$.
(3) 由题意知点 $M(m - 1,2m)$ 的 “$-4$ 级关联点” 为 $N(-4(m - 1)+2m,m - 1+(-4)\times2m)$,
当点 $N$ 在 $y$ 轴上时, $-4(m - 1)+2m = 0$, 解得 $m = 2$,
$\therefore m - 1+(-4)\times2m = -15$, $\therefore N(0,-15)$;
当点 $N$ 在 $x$ 轴上时, $m - 1+(-4)\times2m = 0$,
解得 $m = -\frac{1}{7}$, $\therefore -4(m - 1)+2m = \frac{30}{7}$, $\therefore N(\frac{30}{7},0)$.
综上所述, 点 $N$ 的坐标为$(0,-15)$ 或$(\frac{30}{7},0)$.
查看更多完整答案,请扫码查看


