《2025年5年中考3年模拟八年级数学下册湘教版》

8.(2024湖南长沙一模,8,★★☆)如图所示的是某学校人行入口的智能闸机及其示意图,当它关闭时,双侧挡板边缘的端点A与B之间的距离为10 cm(点A、B在同一水平线上),挡板边缘AC = BD = 70 cm,且与闸机侧立面的夹角∠PCA = ∠BDQ = 30°.当挡板收起后,可以通过闸机的物体的最大宽度为 ( )

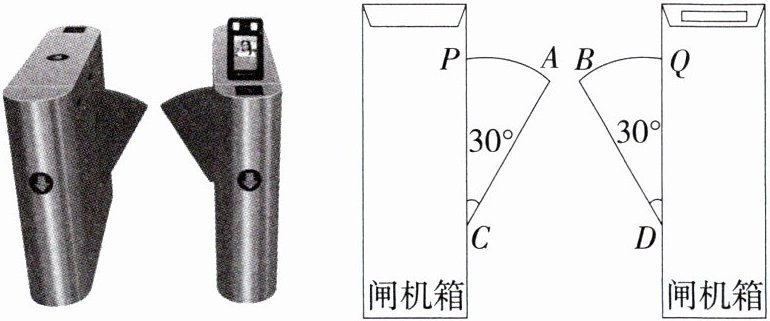
A.(70$\sqrt{2}$+10)cm
B.80 cm
C.(70$\sqrt{3}$+10)cm
D.90 cm

答案：
B 过点A作AE⊥CP于点E，过点B作BF⊥DQ于点F，如图，
在Rt△ACE中，
∵∠ACE = 30°，
∴AE = $\frac{1}{2}AC=\frac{1}{2}×70 = 35$(cm)，同理可得，BF = 35 cm，
∵关闭时，双侧挡板边缘的端点A与B之间的距离为10 cm，
∴当双侧挡板收起时，可以通过闸机的物体的最大宽度为35 + 35 + 10 = 80(cm)，故选B.

9.(2023湖南邵阳绥宁期中,16,★☆☆)如图,在△ABC中,∠ACB = 90°,∠A = 30°,BC = 4 cm,D为AB的中点,则CD的长为________.

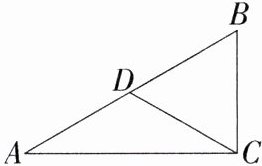
答案： 答案 4 cm
解析
∵∠ACB = 90°，∠A = 30°，BC = 4 cm，
∴AB = 2BC = 8 cm，
∵在Rt△ABC中，D为AB的中点，
∴CD = $\frac{1}{2}AB = 4$ cm.

10.(2023湖南常德鼎城期末,18,★★☆)如图所示,CD⊥AB,垂足为D,∠ACB = 90°,∠A = 30°,求证:BD=$\frac{1}{4}$AB.(M8201001)

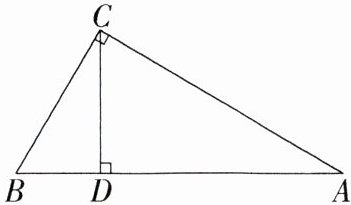
答案： 证明
∵∠ACB = 90°，∠A = 30°，
∴BC = $\frac{1}{2}AB$，
∵CD⊥AB，
∴∠CDB = ∠B + ∠BCD = 90°，
∵∠A + ∠B = 90°，
∴∠BCD = ∠A = 30°，
∴BD = $\frac{1}{2}BC=\frac{1}{2}×\frac{1}{2}AB=\frac{1}{4}AB$，即BD = $\frac{1}{4}AB$.

11.推理能力 如图,在Rt△ABC中,∠C = 90°,∠A = 30°,BC = 12 cm.AB边上一动点P从点A出发沿AB向点B运动,到达B点时停止,BC边上一动点Q从点B出发沿BC向点C运动,到达C点时停止.如果动点P,Q分别以2 cm/s,1 cm/s的速度同时出发,设运动时间为t s,解答下列问题:
(1)当t的值为多少时,△PBQ是等边三角形?
(2)当t的值为多少时,△PBQ是直角三角形? 请说明理由.

答案： 解析 （1）由题意知∠B = 60°，
∴当BQ = BP时，△PBQ是等边三角形.
∵在Rt△ABC中，∠C = 90°，∠A = 30°，BC = 12 cm，
∴AB = 24 cm，易知AP = 2t cm，BQ = t cm，
∴BP = (24 - 2t)cm，
∵BP = BQ，
∴24 - 2t = t，
∴t = 8，
即当t的值为8时，△PBQ是等边三角形.
（2）当t的值为6或$\frac{48}{5}$时，△PBQ是直角三角形.
理由：由（1）知BP = (24 - 2t)cm，∠B = 60°，BQ = t cm，
∵△PBQ是直角三角形，
∴当∠PQB = 90°时，BP = 2BQ，
∴24 - 2t = 2t，解得t = 6；
当∠QPB = 90°时，BQ = 2BP，
∴t = 2(24 - 2t)，解得t = $\frac{48}{5}$.
∴当t的值为6或$\frac{48}{5}$时，△PBQ是直角三角形.