《2025年5年中考3年模拟八年级数学下册湘教版》

8.(2023湖北天门期末,10,★★☆)如图，在平面直角坐标系中，A(8,0)，B(-4,0)，C(8,8)，D(-4,12)，点E在x轴上，满足∠BED = ∠DEC，则点E的坐标为 ( )

A.(2,0)
B.(6,0)
C.(8,0)
D.(2,0)或(8,0)

答案：
D：分两种情况：
①如图 1，过 D 作 DT⊥AC 交 AC 的延长线于点 T，
∵A(8,0)，B(-4,0)，C(8,8)，D(-4,12)，
∴∠DBA = ∠BAT = ∠ATD = 90°，BD = BA = 12，
∴ 四边形 ABDT 是正方形，连接 AD，则∠BAD = ∠TAD = 45°，
∴ 当 E，A 重合时，有∠BED = ∠DEC，
∴E 点的坐标为(8,0).
②如图 2，连接 DE，CE，过 D 作 DH⊥EC 于点 H，作 DT⊥AC 交 AC 的延长线于点 T.
∵∠BED = ∠DEC，DB⊥BE，DE = DE，
∴△BDE≌△HDE(AAS)，
∴BE = HE，DB = DH = 12，由①知四边形 ABDT 是正方形，
∴BD = DT = AB = AT = 12，
∴DH = DT = 12，又
∵CD = CD，
∴Rt△DTC≌Rt△DHC(HL)，
∴CT = CH，
∵AC = 8，
∴CT = CH = AT - AC = 4，设 BE = x，则 HE = x，AE = AB - BE = 12 - x，
∴CE = HE + CH = x + 4，在 Rt△AEC 中，由勾股定理得 AE² + AC² = CE²，即(12 - x)² + 8² = (x + 4)²，解得 x = 6，
∴BE = 6，
∴OE = BE - OB = 6 - 4 = 2，此时 E(2,0). 综上所述，E(2,0)或(8,0)，故选 D.

9.(2024广西河池期中,24,★★☆)已知A(0,1)，B(2,0)，C(4,3).

(1)在坐标系中描出各点，画出△ABC.
(2)求△ABC的面积.
(3)若点P在坐标轴上，且△ABP与△ABC的面积相等，求点P的坐标.

答案：
解析：
(1) 如图所示.

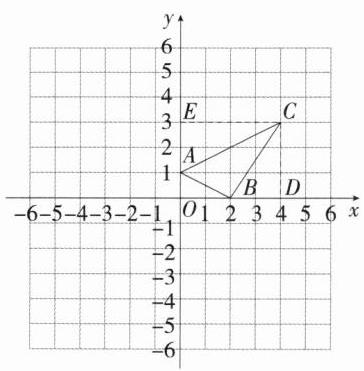
(2) 过点 C 作 x 轴、y 轴的垂线，垂足分别为点 D、E. $S_{四边形DOEC}$ = 3×4 = 12，$S_{\triangle BCD}$ = $\frac{1}{2}$×2×3 = 3，$S_{\triangle ACE}$ = $\frac{1}{2}$×2×4 = 4，$S_{\triangle AOB}$ = $\frac{1}{2}$×2×1 = 1.
∴$S_{\triangle ABC}$ = $S_{四边形DOEC}$ - $S_{\triangle BCD}$ - $S_{\triangle ACE}$ - $S_{\triangle AOB}$ = 12 - 3 - 4 - 1 = 4.
(3) ①当点 P 在 x 轴上时，$S_{\triangle ABP}$ = $\frac{1}{2}$AO·BP = 4，即$\frac{1}{2}$×1×BP = 4，解得 BP = 8，所以点 P 的坐标为(10,0)或(-6,0)；
②当点 P 在 y 轴上时，$S_{\triangle ABP}$ = $\frac{1}{2}$BO·AP = 4，即$\frac{1}{2}$×2×AP = 4，解得 AP = 4，所以点 P 的坐标为(0,5)或(0,-3). 综上所述，点 P 的坐标为(0,5)或(0,-3)或(10,0)或(-6,0).

10.几何直观 如图，平面直角坐标系中，四边形ABCD为矩形，其中，点A、C的坐标分别为(-4,2)、(1,-4)，且AD//x轴，交y轴于点M，AB交x轴于点N.一动点P从A出发，以每秒$\frac{1}{2}$个单位的速度沿AB向B点运动.
(1)求B、D两点的坐标和矩形ABCD的面积.
(2)在P点运动过程中，连接MP、OP，则∠AMP、∠MPO、∠PON有怎样的数量关系?
(3)是否存在某一时刻t，使三角形AMP的面积等于矩形ABCD面积的$\frac{1}{3}$?若存在，求出t的值及此时点P的坐标；若不存在，请说明理由.

答案：
解析：
(1)
∵ 点 A、C 的坐标分别为(-4,2)、(1,-4)，四边形 ABCD 为矩形，AD//x 轴，
∴B(-4,-4)，D(1,2)，
∴$S_{矩形ABCD}$ = (1 + 4)×(2 + 4) = 30.
(2) 当点 P 在线段 AN 上时，作 PQ//AM 交 y 轴于点 Q，如图，
∵AM//ON，
∴AM//PQ//ON，
∴∠QPM = ∠AMP，∠QPO = ∠PON，
∴∠QPM + ∠QPO = ∠AMP + ∠PON，即∠MPO = ∠AMP + ∠PON；当点 P 在线段 NB 上时，同样方法可得∠MPO = ∠AMP - ∠PON.
(3) 存在.
∵AM = 4，AP = $\frac{1}{2}$t，
∴$S_{\triangle AMP}$ = $\frac{1}{2}$×4×$\frac{1}{2}$t = t，
∵ 三角形 AMP 的面积等于矩形 ABCD 面积的$\frac{1}{3}$，
∴t = 30×$\frac{1}{3}$ = 10，
∴AP = $\frac{1}{2}$×10 = 5，
∵AN = 2，
∴NP = 3，则点 P 坐标为(-4,-3).