第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
9.(2023湖南常德中考,7,★★☆)如图,在正方形ABCD中,对角线AC和BD相交于点O,E,F分别为AO,DO上的点,且EF//AD,连接AF,DE.若∠FAC = 15°,则∠AED的度数为 ( )

A.80°
B.90°
C.105°
D.115°

A.80°
B.90°
C.105°
D.115°
答案:
C \n因为四边形 $ABCD$ 为正方形,所以 $OA = OD$,$\angle OBC=\angle OCB=\angle OAD=\angle ODA = 45^{\circ}$,易得 $EF// BC$;\n所以 $\angle OEF=\angle OCB = 45^{\circ}$,$\angle OFE=\angle OBC = 45^{\circ}$;\n所以 $\angle OEF=\angle OFE = 45^{\circ}$,所以 $\angle AEF=\angle DFE = 135^{\circ}$,$OE = OF$;\n因为 $OA = OD$,所以 $AE = DF$,又因为 $EF = EF$,所以 $\triangle AEF\cong\triangle DFE(SAS)$;\n所以 $\angle CAF=\angle FDE = 15^{\circ}$,所以 $\angle ADE=\angle ODA-\angle FDE=45^{\circ}-15^{\circ}=30^{\circ}$;\n所以 $\angle AED=180^{\circ}-\angle OAD-\angle ADE=180^{\circ}-45^{\circ}-30^{\circ}=105^{\circ}$. 故选 C.
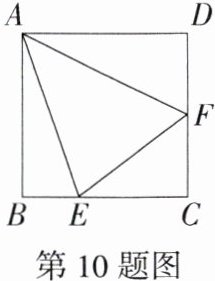
10.半角模型(2023重庆中考A卷,9,★★☆)如图,在正方形ABCD中,点E,F分别在BC,CD上,连接AE,AF,EF,∠EAF = 45°.若∠BAE = $\alpha$,则∠FEC = ( )
A.2$\alpha$
B.90° - 2$\alpha$
C.45° - $\alpha$
D.90° - $\alpha$

A.2$\alpha$
B.90° - 2$\alpha$
C.45° - $\alpha$
D.90° - $\alpha$
答案:
A \n因为四边形 $ABCD$ 是正方形,所以 $AD = AB$,$\angle BAD=\angle ABC=\angle ADC = 90^{\circ}$,将 $\triangle ADF$ 绕点 $A$ 顺时针旋转 $90^{\circ}$ 得 $\triangle ABG$,如图所示;\n则 $AF = AG$,$\angle DAF=\angle BAG$,因为 $\angle EAF = 45^{\circ}$,所以 $\angle BAE+\angle DAF = 45^{\circ}$;\n所以 $\angle GAE=\angle FAE = 45^{\circ}$,在 $\triangle GAE$ 和 $\triangle FAE$ 中,$\begin{cases}AG = AF\\\angle GAE=\angle FAE\\AE = AE\end{cases}$;\n所以 $\triangle GAE\cong\triangle FAE(SAS)$,所以 $\angle AEF=\angle AEG$;\n因为 $\angle BAE=\alpha$,所以 $\angle AEB = 90^{\circ}-\alpha$,所以 $\angle AEF=\angle AEB = 90^{\circ}-\alpha$;\n所以 $\angle FEC=180^{\circ}-\angle AEF-\angle AEB=180^{\circ}-2\times(90^{\circ}-\alpha)=2\alpha$,故选 A.

A \n因为四边形 $ABCD$ 是正方形,所以 $AD = AB$,$\angle BAD=\angle ABC=\angle ADC = 90^{\circ}$,将 $\triangle ADF$ 绕点 $A$ 顺时针旋转 $90^{\circ}$ 得 $\triangle ABG$,如图所示;\n则 $AF = AG$,$\angle DAF=\angle BAG$,因为 $\angle EAF = 45^{\circ}$,所以 $\angle BAE+\angle DAF = 45^{\circ}$;\n所以 $\angle GAE=\angle FAE = 45^{\circ}$,在 $\triangle GAE$ 和 $\triangle FAE$ 中,$\begin{cases}AG = AF\\\angle GAE=\angle FAE\\AE = AE\end{cases}$;\n所以 $\triangle GAE\cong\triangle FAE(SAS)$,所以 $\angle AEF=\angle AEG$;\n因为 $\angle BAE=\alpha$,所以 $\angle AEB = 90^{\circ}-\alpha$,所以 $\angle AEF=\angle AEB = 90^{\circ}-\alpha$;\n所以 $\angle FEC=180^{\circ}-\angle AEF-\angle AEB=180^{\circ}-2\times(90^{\circ}-\alpha)=2\alpha$,故选 A.

11.(2024湖南长沙雅礼教育集团期中,10,★★☆)如图,已知四边形ABCD和四边形CEFG均为正方形,且G是AB的中点,连接AE,若AB = 4,则AE的长为 ( )

A.2$\sqrt{5}$
B.4$\sqrt{5}$
C.5
D.2$\sqrt{17}$

A.2$\sqrt{5}$
B.4$\sqrt{5}$
C.5
D.2$\sqrt{17}$
答案:
D \n如图,过点 $E$ 作 $EM\perp AD$ 交 $BC$ 于点 $N$,交 $AD$ 于点 $M$,四边形 $ABNM$ 是矩形,则 $MN = AB = 4$;\n因为 $G$ 是 $AB$ 的中点,所以 $BG=\frac{1}{2}AB = 2$;\n因为四边形 $ABCD$ 和四边形 $CEFG$ 均为正方形,所以 $CG = CE$,$\angle B = 90^{\circ}=\angle CNE$,$\angle GCE = 90^{\circ}$;\n所以 $\angle BCG+\angle BCE=\angle BCE+\angle CEN = 90^{\circ}$,所以 $\angle BCG=\angle CEN$;\n所以 $\triangle BCG\cong\triangle NEC(AAS)$,所以 $NE = BC = 4$,$CN = BG = 2$;\n所以 $ME = 8$,$AM = BN = 2$,所以 $AE=\sqrt{8^{2}+2^{2}}=\sqrt{68}=2\sqrt{17}$.
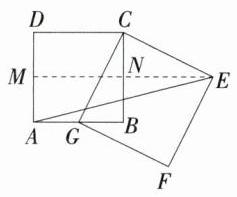
D \n如图,过点 $E$ 作 $EM\perp AD$ 交 $BC$ 于点 $N$,交 $AD$ 于点 $M$,四边形 $ABNM$ 是矩形,则 $MN = AB = 4$;\n因为 $G$ 是 $AB$ 的中点,所以 $BG=\frac{1}{2}AB = 2$;\n因为四边形 $ABCD$ 和四边形 $CEFG$ 均为正方形,所以 $CG = CE$,$\angle B = 90^{\circ}=\angle CNE$,$\angle GCE = 90^{\circ}$;\n所以 $\angle BCG+\angle BCE=\angle BCE+\angle CEN = 90^{\circ}$,所以 $\angle BCG=\angle CEN$;\n所以 $\triangle BCG\cong\triangle NEC(AAS)$,所以 $NE = BC = 4$,$CN = BG = 2$;\n所以 $ME = 8$,$AM = BN = 2$,所以 $AE=\sqrt{8^{2}+2^{2}}=\sqrt{68}=2\sqrt{17}$.

12.(2024贵州黔东南州二模,16,★★☆)如图,以Rt△ABC的三条边为边,向三角形ABC的外侧分别作正方形,连接CG,其中AC = 1,BC = 2,则CG的长为________.
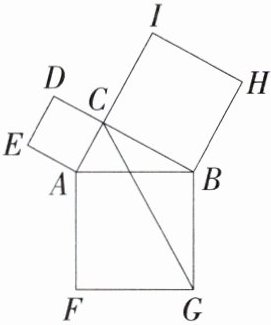

答案:
答案 $\sqrt{13}$\n**解析** 如图,连接 $AH$,因为四边形 $ABGF$ 和四边形 $BCIH$ 是正方形,所以 $BH = HI = IC=BC = 2$,$AB = BG$,$\angle ABG=\angle HBC=\angle CIH = 90^{\circ}$;\n所以 $\angle ABC+\angle ABG=\angle ABC+\angle HBC$,所以 $\angle ABH=\angle CBG$;\n所以 $\triangle ABH\cong\triangle GBC(SAS)$,所以 $HA = CG$;\n因为 $\angle ACB = 90^{\circ}$,所以 $\angle ACB+\angle ICB = 180^{\circ}$,所以 $A$、$C$、$I$ 三点在同一条直线上,所以 $AI=AC + CI=1 + 2 = 3$;\n所以 $HA=\sqrt{HI^{2}+AI^{2}}=\sqrt{2^{2}+3^{2}}=\sqrt{13}$,所以 $CG$ 的长为 $\sqrt{13}$.

答案 $\sqrt{13}$\n**解析** 如图,连接 $AH$,因为四边形 $ABGF$ 和四边形 $BCIH$ 是正方形,所以 $BH = HI = IC=BC = 2$,$AB = BG$,$\angle ABG=\angle HBC=\angle CIH = 90^{\circ}$;\n所以 $\angle ABC+\angle ABG=\angle ABC+\angle HBC$,所以 $\angle ABH=\angle CBG$;\n所以 $\triangle ABH\cong\triangle GBC(SAS)$,所以 $HA = CG$;\n因为 $\angle ACB = 90^{\circ}$,所以 $\angle ACB+\angle ICB = 180^{\circ}$,所以 $A$、$C$、$I$ 三点在同一条直线上,所以 $AI=AC + CI=1 + 2 = 3$;\n所以 $HA=\sqrt{HI^{2}+AI^{2}}=\sqrt{2^{2}+3^{2}}=\sqrt{13}$,所以 $CG$ 的长为 $\sqrt{13}$.

13.(2024四川宜宾中考,18,★★☆)如图,正方形ABCD的边长为1,M、N是边BC、CD上的动点.若∠MAN = 45°,则MN的最小值为________.(M8202005)


答案:
答案 $2\sqrt{2}-2$\n**解析** 如图,延长 $CD$ 到点 $G$,使 $DG = BM$,连接 $AG$.\n因为四边形 $ABCD$ 为正方形,所以 $AD = AB$,$\angle MBA=\angle ADC = 90^{\circ}$,所以 $\angle ADG = 90^{\circ}=\angle ABM$;\n又因为 $BM = DG$,所以 $\triangle ABM\cong\triangle ADG(SAS)$,所以 $\angle BAM=\angle DAG$,$AM = AG$;\n因为 $\angle MAN = 45^{\circ}$,所以 $\angle BAM+\angle DAN = 45^{\circ}$,所以 $\angle DAG+\angle DAN = 45^{\circ}$,即 $\angle GAN = 45^{\circ}$;\n在 $\triangle GAN$ 和 $\triangle MAN$ 中,$\begin{cases}AG = AM\\\angle GAN=\angle MAN\\AN = AN\end{cases}$,所以 $\triangle GAN\cong\triangle MAN(SAS)$,所以 $GN = MN$.\n设 $BM = x$,$MN = y$,则 $GN = y$,$DG = x$. 因为 $BC = CD = 1$,所以 $CM = 1 - x$,$CN=x - y + 1$;\n在 $Rt\triangle CMN$ 中,由勾股定理得 $MN^{2}=CM^{2}+CN^{2}$,即 $y^{2}=(1 - x)^{2}+(x - y + 1)^{2}$;\n整理可得 $y=\frac{x^{2}+1}{x + 1}=\frac{(x + 1)^{2}-2(x + 1)+2}{x + 1}=x + 1+\frac{2}{x + 1}-2$;\n因为 $(\sqrt{x + 1}-\sqrt{\frac{2}{x + 1}})^{2}\geq0$,所以 $x + 1+\frac{2}{x + 1}\geq2\sqrt{(x + 1)\cdot\frac{2}{x + 1}}=2\sqrt{2}$;\n所以 $y\geq2\sqrt{2}-2$,当 $y = 2\sqrt{2}-2$ 时,$\sqrt{x + 1}=\sqrt{\frac{2}{x + 1}}$,解得 $x=\sqrt{2}-1$(负舍),符合题意,故 $MN$ 的最小值为 $2\sqrt{2}-2$.
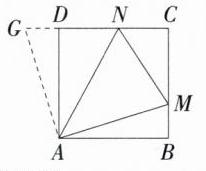
答案 $2\sqrt{2}-2$\n**解析** 如图,延长 $CD$ 到点 $G$,使 $DG = BM$,连接 $AG$.\n因为四边形 $ABCD$ 为正方形,所以 $AD = AB$,$\angle MBA=\angle ADC = 90^{\circ}$,所以 $\angle ADG = 90^{\circ}=\angle ABM$;\n又因为 $BM = DG$,所以 $\triangle ABM\cong\triangle ADG(SAS)$,所以 $\angle BAM=\angle DAG$,$AM = AG$;\n因为 $\angle MAN = 45^{\circ}$,所以 $\angle BAM+\angle DAN = 45^{\circ}$,所以 $\angle DAG+\angle DAN = 45^{\circ}$,即 $\angle GAN = 45^{\circ}$;\n在 $\triangle GAN$ 和 $\triangle MAN$ 中,$\begin{cases}AG = AM\\\angle GAN=\angle MAN\\AN = AN\end{cases}$,所以 $\triangle GAN\cong\triangle MAN(SAS)$,所以 $GN = MN$.\n设 $BM = x$,$MN = y$,则 $GN = y$,$DG = x$. 因为 $BC = CD = 1$,所以 $CM = 1 - x$,$CN=x - y + 1$;\n在 $Rt\triangle CMN$ 中,由勾股定理得 $MN^{2}=CM^{2}+CN^{2}$,即 $y^{2}=(1 - x)^{2}+(x - y + 1)^{2}$;\n整理可得 $y=\frac{x^{2}+1}{x + 1}=\frac{(x + 1)^{2}-2(x + 1)+2}{x + 1}=x + 1+\frac{2}{x + 1}-2$;\n因为 $(\sqrt{x + 1}-\sqrt{\frac{2}{x + 1}})^{2}\geq0$,所以 $x + 1+\frac{2}{x + 1}\geq2\sqrt{(x + 1)\cdot\frac{2}{x + 1}}=2\sqrt{2}$;\n所以 $y\geq2\sqrt{2}-2$,当 $y = 2\sqrt{2}-2$ 时,$\sqrt{x + 1}=\sqrt{\frac{2}{x + 1}}$,解得 $x=\sqrt{2}-1$(负舍),符合题意,故 $MN$ 的最小值为 $2\sqrt{2}-2$.

14.(2024湖南湘潭岳塘期中,21,★★☆)如图,已知正方形ABCD中,AB = 4,点M在边CD上,射线AM交BD于点E,交射线BC于点F,连接CE,过点C作CP⊥CE交AF于点P.
(1)求证:△ADE≌△CDE.
(2)判断△CPF的形状,并说明理由.
(3)作DM的中点N,连接PN,若PN = 3,求CF的长.
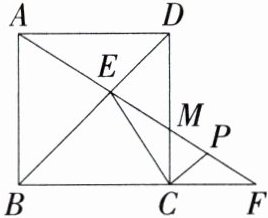
(1)求证:△ADE≌△CDE.
(2)判断△CPF的形状,并说明理由.
(3)作DM的中点N,连接PN,若PN = 3,求CF的长.

答案:
解析 \n
(1) **证明**:因为四边形 $ABCD$ 是正方形,所以 $AD = CD$,$\angle ADE=\angle CDE = 45^{\circ}$;\n在 $\triangle ADE$ 和 $\triangle CDE$ 中,$\begin{cases}AD = CD\\\angle ADE=\angle CDE\\DE = DE\end{cases}$,所以 $\triangle ADE\cong\triangle CDE(SAS)$.\n
(2) $\triangle CPF$ 是等腰三角形. 理由如下:\n因为 $\triangle ADE\cong\triangle CDE$,所以 $\angle DAE=\angle DCE$;\n因为 $CP\perp CE$,$DC\perp CF$,所以 $\angle PCE=\angle DCF$,所以 $\angle DCE=\angle PCF$;\n因为 $AD// BF$,所以 $\angle DAE=\angle CFP$,所以 $\angle PCF=\angle CFP$,所以 $CP = PF$,所以 $\triangle CPF$ 是等腰三角形.\n
(3) 如图,连接 $DF$,因为 $\angle PCF=\angle PFC$,所以 $\angle PCM=\angle PMC$,所以 $PC = MP$,所以 $MP = PF$;\n又因为点 $N$ 是 $DM$ 的中点,所以 $PN$ 是 $\triangle MDF$ 的中位线;\n所以 $DF = 2PN = 6$,所以 $CF=\sqrt{DF^{2}-CD^{2}}=2\sqrt{5}$.
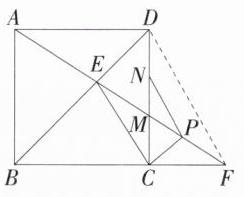
解析 \n
(1) **证明**:因为四边形 $ABCD$ 是正方形,所以 $AD = CD$,$\angle ADE=\angle CDE = 45^{\circ}$;\n在 $\triangle ADE$ 和 $\triangle CDE$ 中,$\begin{cases}AD = CD\\\angle ADE=\angle CDE\\DE = DE\end{cases}$,所以 $\triangle ADE\cong\triangle CDE(SAS)$.\n
(2) $\triangle CPF$ 是等腰三角形. 理由如下:\n因为 $\triangle ADE\cong\triangle CDE$,所以 $\angle DAE=\angle DCE$;\n因为 $CP\perp CE$,$DC\perp CF$,所以 $\angle PCE=\angle DCF$,所以 $\angle DCE=\angle PCF$;\n因为 $AD// BF$,所以 $\angle DAE=\angle CFP$,所以 $\angle PCF=\angle CFP$,所以 $CP = PF$,所以 $\triangle CPF$ 是等腰三角形.\n
(3) 如图,连接 $DF$,因为 $\angle PCF=\angle PFC$,所以 $\angle PCM=\angle PMC$,所以 $PC = MP$,所以 $MP = PF$;\n又因为点 $N$ 是 $DM$ 的中点,所以 $PN$ 是 $\triangle MDF$ 的中位线;\n所以 $DF = 2PN = 6$,所以 $CF=\sqrt{DF^{2}-CD^{2}}=2\sqrt{5}$.

查看更多完整答案,请扫码查看


