《2025年5年中考3年模拟八年级数学下册湘教版》

1.如图,OP为∠AOB的平分线,PC⊥OA,PD⊥OB,垂足分别为C,D,则下列结论错误的是 ( )


A.PC = PD
B.∠CPO = ∠DOP
C.∠CPO = ∠DPO
D.OC = OD

答案： B

∵OP为∠AOB的平分线，PC⊥OA，PD⊥OB，
∴PC = PD，在Rt△OPC和Rt△OPD中，$\begin{cases}OP = OP\\PC = PD\end{cases}$，
∴Rt△OPC≌Rt△OPD(HL)，
∴OC = OD，∠CPO = ∠DPO≠∠DOP，
∴选项B结论错误. 故选B.

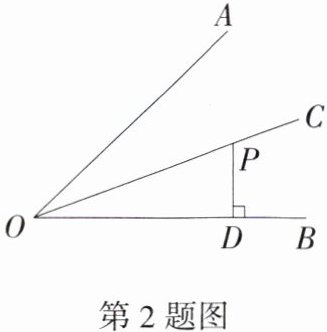
2.(2024青海中考)如图,OC平分∠AOB,点P在OC上,PD⊥OB,PD = 2,则点P到OA的距离是 ( )(M8201005)

A.4
B.3
C.2
D.1

答案：
C 如图，过点P作PE⊥AO于点E，
∵OC平分∠AOB，点P在OC上，PD⊥OB，
∴PE = PD = 2，
∴点P到OA的距离是2. 故选C.

3.如图,在△ABC中,∠ACB = 90°,AD是△ABC的角平分线,BC = 10 cm,BD : DC = 3 : 2,则点D到AB的距离为________.

答案： 答案 4 cm
解析
∵BC = 10 cm，BD : DC = 3 : 2，
∴DC = $10\times\frac{2}{3 + 2}=4$ cm，
∵AD是△ABC的角平分线，∠ACB = 90°，
∴点D到AB的距离等于DC的长，即点D到AB的距离为4 cm. 故答案为4 cm.

4.如图,在△ABC中,∠C = 90°,AD平分∠CAB,DE⊥AB于点E,点F在AC上,BE = FC.求证:BD = DF.(M8201005)

答案： 证明
∵AD平分∠CAB，DE⊥AB，∠C = 90°，
∴DC = DE.
在△DCF和△DEB中，$\begin{cases}DC = DE\\\angle C = \angle DEB\\CF = EB\end{cases}$，
∴△DCF≌△DEB(SAS)，
∴BD = DF.

5.下图是一个风筝骨架的示意图.为使风筝平衡,须使∠AOP = ∠BOP.我们已知PC⊥OA于点C,PD⊥OB于点D,那么PC和PD应满足________,才能保证OP为∠AOB的平分线.

答案： 答案 PC = PD
解析
∵PC⊥OA，PD⊥OB，
∴∠PCO = ∠PDO = 90°，
∵OP = OP，PC = PD，
∴Rt△PCO≌Rt△PDO(HL)，
∴∠AOP = ∠BOP.
∴PC和PD应满足PC = PD，才能保证OP为∠AOB的平分线.

6.如图,在四边形ABCD中,AD⊥AB,连接BD,∠ABD = 35°,BD⊥CD,过点D作DP⊥BC于点P,若AD = PD,则∠C的度数为________.

答案： 答案 55°
解析
∵AD⊥AB，DP⊥BC，AD = PD，
∴BD是∠ABC的平分线，
∴∠DBC = ∠ABD = 35°.
∵BD⊥CD，
∴∠BDC = 90°，
∴∠C = 90° - ∠DBC = 90° - 35° = 55°.

7.(2022湖南岳阳临湘期中)如图,P是OC上一点,PD⊥OA于点D,PE⊥OB于点E,F、G分别是OA、OB上的点,且PF = PG,DF = EG.求证:OC平分∠AOB.(M8201005)

答案： 证明 在Rt△PFD和Rt△PGE中，$\begin{cases}PF = PG\\DF = EG\end{cases}$，
∴Rt△PFD≌Rt△PGE(HL)，
∴PD = PE，
∵P是OC上一点，PD⊥OA，PE⊥OB，
∴OC平分∠AOB.

8.(2024湖南长沙望城模拟,8,★★☆)如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE = DG,则∠AED + ∠AGD = ( )

A.180°
B.200°
C.210°
D.240°

答案：
A 过D点作DH⊥AC于点H，如图，
∵AD是△ABC的角平分线，DF⊥AB，DH⊥AC，
∴DF = DH，
在Rt△DFE和Rt△DHG中，$\begin{cases}DE = DG\\DF = DH\end{cases}$，
∴Rt△DFE≌Rt△DHG(HL)，
∴∠DEF = ∠DGH，
∵∠AED + ∠DEF = 180°，
∴∠AED + ∠AGD = 180°. 故选A.