《2025年5年中考3年模拟八年级数学下册湘教版》

1.在Rt△ABC中，∠C = 90°。若a = 6，b = 8，则c的值是(M8201003) （ ）
A.10
B.2$\sqrt{34}$
C.2$\sqrt{7}$
D.4.8

答案： A 在 Rt△ABC 中，∠C = 90°，a = 6，b = 8，
由勾股定理得 $c=\sqrt{a^{2}+b^{2}}=\sqrt{6^{2}+8^{2}} = 10$，故选 A.
·易错警示
本题中明确告知了 c 为斜边，所以可以直接利用勾股定理求长度.如果题目中没有明确告知斜边是哪条边，需要注意分类讨论.

2.(2024广西防城港防城月考)如图，数字9和16分别代表所在正方形的面积，则A所代表的正方形的面积为 （ ）

A.5
B.25
C.27
D.5$\sqrt{2}$

答案： B 由勾股定理可知 $S_{A}=9 + 16 = 25$，故选 B.

3.(2024湖南长沙宁乡期中)我们在学习“实数”时画了这样一个图：以数轴上1个单位长度为边长作一个正方形，然后以原点O为圆心，正方形的对角线长为半径画弧交数轴于点A，如图所示的线段OA的长度是________.

答案： 答案 $\sqrt{2}$
解析 由题意，利用勾股定理得，$OA = OB=\sqrt{1^{2}+1^{2}}=\sqrt{2}$.

4.（2024陕西西安雁塔一模，6，★☆☆）如图，在3×3的正方形网格中，每个小正方形的边长均为1，点A，B，C都在格点上，AD为△ABC的边BC上的高，则AD的长为 （ ）

A.$\frac{7\sqrt{10}}{15}$
B.$\frac{7\sqrt{10}}{5}$
C.$\frac{7\sqrt{10}}{20}$
D.$\frac{7\sqrt{10}}{10}$

答案： D 由题意可得，$S_{\triangle ABC}=3\times3-\frac{1}{2}\times1\times3-\frac{1}{2}\times2\times3-\frac{1}{2}\times1\times2=\frac{7}{2}$，$BC=\sqrt{1^{2}+3^{2}}=\sqrt{10}$，
$\therefore\frac{1}{2}\times\sqrt{10}AD=\frac{7}{2}$，$\therefore AD=\frac{7\sqrt{10}}{10}$，故选 D.
·方法归纳
网格问题是热点考向之一，常常考查网格作图、网格中求线段长或角度等问题.一般先利用勾股定理求得线段的长，再结合几何性质进行几何推理得到角度关系，而在求三角形的高时，往往需要借助网格求得三角形的面积和相应线段的长，再利用三角形面积公式来求解.

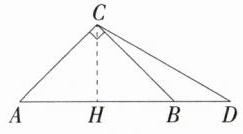
5.(2024安徽中考，7，★☆☆)如图，在Rt△ABC中，AC = BC = 2，点D在AB的延长线上，且CD = AB，则BD的长是(M8201003) （ ）

A.$\sqrt{10}-\sqrt{2}$
B.$\sqrt{6}-\sqrt{2}$
C.2$\sqrt{2}-2$
D.2$\sqrt{2}-\sqrt{6}$

答案：
B 如图，过点 C 作 $CH\perp AB$
于 H，$\because AC = BC = 2$，$\angle ACB = 90^{\circ}$，$CH\perp AB$，
$\therefore AB = 2\sqrt{2}$，$AH = BH = CH=\sqrt{2}$，
$\because CD = AB = 2\sqrt{2}$，
$\therefore DH=\sqrt{CD^{2}-CH^{2}}=\sqrt{8 - 2}=\sqrt{6}$，$\therefore DB=\sqrt{6}-\sqrt{2}$.

6.(易错题)(2024广西钦州浦北期中，17，★☆☆)如图，∠CAB = 45°，点D在射线AB上，且AD = 4，点P在射线AC上运动，当△ADP是直角三角形时，PD的长为________.

答案： 答案 4 或 $2\sqrt{2}$
解析 $\because\triangle ADP$是直角三角形，$\angle CAB = 45^{\circ}$，$\therefore$只有两种情况，①当 $\angle ADP = 90^{\circ}$时，$\because\angle CAB = 45^{\circ}$，$\therefore PD = AD = 4$；
②当 $\angle APD = 90^{\circ}$时，$\because\angle CAB = 45^{\circ}$，$\therefore PD = AP$，
$\because$在 Rt△ADP 中，$AP^{2}+PD^{2}=AD^{2}$，即 $2PD^{2}=4^{2}$，
$\therefore PD = 2\sqrt{2}$.故 PD 的长为 4 或 $2\sqrt{2}$.
·易错警示
本题要区分哪个角为直角，分两种情况讨论，避免漏解.

7.(2022浙江杭州中考，21，★★☆)如图，在Rt△ACB中，∠ACB = 90°，点M为边AB的中点，点E在线段AM上，EF⊥AC于点F，连接CM，CE.已知∠A = 50°，∠ACE = 30°.(M8201003)
(1)求证：CE = CM.
(2)若AB = 4，求线段FC的长.

答案： 解析
(1)证明：$\because\angle ACB = 90^{\circ}$，$\angle A = 50^{\circ}$，点 M 为边 AB 的中点，$\therefore\angle B = 40^{\circ}$，$CM = MA = MB$，
$\therefore\angle MCB=\angle B = 40^{\circ}$，$\therefore\angle EMC=\angle MCB+\angle B = 80^{\circ}$，
$\because\angle ACE = 30^{\circ}$，$\therefore\angle MEC=\angle A+\angle ACE = 80^{\circ}$，
$\therefore\angle MEC=\angle EMC$，$\therefore CE = CM$.
(2)$\because AB = 4$，$\therefore CE = CM=\frac{1}{2}AB = 2$，
$\because EF\perp AC$，$\angle ACE = 30^{\circ}$，$\therefore EF=\frac{1}{2}CE = 1$，
在 Rt△EFC 中，由勾股定理得 $FC=\sqrt{CE^{2}-EF^{2}}=\sqrt{2^{2}-1^{2}}=\sqrt{3}$.