《2025年5年中考3年模拟八年级数学下册湘教版》

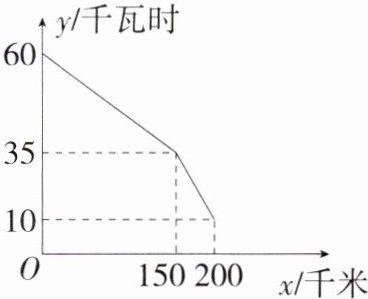
5.(2024湖南长沙模拟)新能源汽车作为一个新兴产业,摆脱了汽车对石油的依赖,而且没有废气排放,发展新能源是保障国家环境安全及能源安全的重要措施.如图所示的是某型号新能源纯电动汽车充满电后,蓄电池剩余电量$y$(千瓦时)关于已行驶路程$x$(千米)的函数图象.(M8204006)
(1)根据图象,直接写出蓄电池剩余电量为35千瓦时时的汽车已行驶的路程;当$0\leq x\leq150$时,求汽车每消耗1千瓦时的电量所能行驶的路程.
(2)当$150\leq x\leq200$时,求$y$关于$x$的函数表达式,并计算当汽车已行驶180千米时,蓄电池的剩余电量.

答案： 解析
（1）由题图可知，蓄电池剩余电量为 35 千瓦时时的汽车已行驶的路程为 150 千米。
当 $0\leqslant x\leqslant150$ 时，$\frac{150}{60 - 35}=6$（千米/千瓦时），$\therefore$ 汽车每消耗 1 千瓦时的电量所能行驶的路程是 6 千米。
（2）设当 $150\leqslant x\leqslant200$ 时，$y$ 关于 $x$ 的函数表达式为 $y = kx + b(k\neq0)$。
把 $(150,35)$，$(200,10)$ 代入，得 $\begin{cases}150k + b = 35\\200k + b = 10\end{cases}$，解得 $\begin{cases}k = -\frac{1}{2}\\b = 110\end{cases}$，
$\therefore y = -\frac{1}{2}x + 110(150\leqslant x\leqslant200)$，
当 $x = 180$ 时，$y = -\frac{1}{2}\times180 + 110 = 20$，即蓄电池的剩余电量为 20 千瓦时。

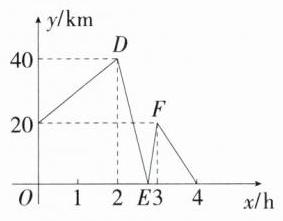
6.(2024山东威海中考,10,★★☆)同一条公路连接$A$,$B$,$C$三地,$B$地在$A$,$C$两地之间.甲、乙两车分别从$A$地、$B$地同时出发前往$C$地.甲车速度始终保持不变,乙车中途休息一段时间后继续行驶.下图是表示甲、乙两车之间的距离$y$(km)与时间$x$(h)的函数关系,则下列结论正确的是（ ）

A.甲车行驶$\frac{8}{3}$h与乙车相遇
B.$A$,$C$两地相距220 km
C.甲车的速度是70 km/h
D.乙车中途休息36分钟

答案：
A
**解析**：根据函数图象可得 $AB$ 两地之间的距离为 $40 - 20 = 20(km)$，两车行驶了 4 小时，同时到达 $C$ 地，如图所示，在 $0\leqslant x\leqslant2$ 时，两车同向运动，在 $x = 2$，即点 $D$ 时，两者距离发生改变，此时乙车休息，$E$ 点表示的实际意义是两车相遇，$F$ 点表示的实际意义是乙车休息后再出发，$\therefore$ 乙车休息了 1 h，故 D 选项不正确，不符合题意；设甲车的速度为 $a\ km/h$，乙车的速度为 $b\ km/h$，根据题意，乙车休息后两者同时到达 $C$ 地，则甲车的速度比乙车的速度慢，$a ＜ b$，$\because2b + 20 - 2a = 40$，即 $b - a = 10$，在 $2\leqslant x\leqslant3$ 时，乙车不动，甲车追上乙车并超过乙车 20 km，$\therefore$ 甲车的速度是 $\frac{40 + 20}{1}=60(km/h)$，$\therefore$ 乙车速度为 $60 + 10 = 70(km/h)$，故 C 选项不正确，不符合题意；$\therefore AC$ 的距离为 $4\times60 = 240(km)$，故 B 选项不正确，不符合题意；设 $x$ 小时后两辆车相遇，依题意得 $60x = 2\times70 + 20$，解得 $x=\frac{8}{3}$，即 $\frac{8}{3}$ 小时后，两车相遇，故 A 选项正确，符合题意. 故选 A。

7.(2024黑龙江齐齐哈尔中考,22,★★☆)领航无人机表演团队进行无人机表演训练,甲无人机以$a$米/秒的速度从地面起飞,乙无人机从距离地面20米高的楼顶起飞,甲、乙两架无人机同时匀速上升,6秒后甲无人机到达训练计划指定的高度停止上升开始表演,完成表演动作后,按原速继续飞行上升,当甲、乙两架无人机按照训练计划准时到达距离地面高度为96米的位置时,进行了时长为$t$秒的联合表演,表演完成后以相同的速度同时返回地面.甲、乙两架无人机所在的位置距离地面的高度$y$(米)与无人机飞行的时间$x$(秒)之间的函数关系如图所示.
请结合图象解答下列问题:(M8204006)
(1)$a$=________,$t$=________.
(2)求线段$MN$所在直线的函数解析式.
(3)两架无人机表演训练到多少秒时,它们距离地面的高度差为12米? (直接写出答案即可)

答案： 解析
（1）由题意得甲无人机的速度为 $a = 48\div6 = 8$（米/秒），$t = 39 - 19 = 20$（秒）。故答案为 8；20。
（2）由图象知，$N(19,96)$，$\because$ 甲无人机的速度为 8 米/秒，$\therefore$ 甲无人机匀速从 0 米到 96 米所用时间为 $96\div8 = 12$（秒），$\therefore$ 甲无人机单独表演所用时间为 $19 - 12 = 7$（秒），$\because6 + 7 = 13$（秒），$\therefore M(13,48)$，设线段 $MN$ 所在直线的函数解析式为 $y = kx + b(k\neq0)$，将 $M(13,48)$，$N(19,96)$ 代入，得 $\begin{cases}13k + b = 48\\19k + b = 96\end{cases}$，解得 $\begin{cases}k = 8\\b = - 56\end{cases}$，$\therefore$ 线段 $MN$ 所在直线的函数解析式为 $y = 8x - 56$。
（3）设 $A(0,20)$，$B(6,48)$，易得线段 $OB$ 所在直线的函数解析式为 $y = 8x$，线段 $AN$ 所在直线的函数解析式为 $y = 4x + 20$，线段 $BM$ 所在直线的函数解析式为 $y = 48$。
当 $0\leqslant t\leqslant6$ 时，由题意得 $|4x + 20 - 8x| = 12$，解得 $x = 2$ 或 $x = 8$（舍去）；
当 $6 ＜ t\leqslant13$ 时，由题意得 $|4x + 20 - 48| = 12$，解得 $x = 10$ 或 $x = 4$（舍去）；
当 $13 ＜ t\leqslant19$ 时，由题意得 $|4x + 20-(8x - 56)| = 12$，解得 $x = 16$ 或 $x = 22$（舍去）。
综上，两架无人机表演训练到第 2 秒，第 10 秒和第 16 秒时，它们距离地面的高度差为 12 米。