《2025年5年中考3年模拟八年级数学下册湘教版》

1.(2024湖南张家界模拟)若一个多边形的内角和是外角和的3倍,则这个多边形的边数是 ( )
A.6
B.7
C.8
D.9

答案： C 多边形的外角和是 360°，设这个多边形的边数是 n，根据题意得 180°·(n - 2)=3×360°，解得 n = 8.

2.一题多解(2023江苏扬州中考)如果一个多边形每一个外角都是60°,那么这个多边形的边数为________.(M8202001)

答案： **答案** 6
**解析** 【解法一】利用外角和：多边形的边数是 360°÷60° = 6.
【解法二】利用内角和：
∵多边形每一个外角都是 60°，
∴多边形每一个内角都是 180° - 60° = 120°，设这个多边形是 n 边形，则(n - 2)×180° = 120°n，解得 n = 6，即这个多边形的边数是 6.

3.新独家原创第五套人民币中的5角硬币色泽为镍白色,正、反面的内周边缘均为正十一边形,则其外角和为 ( )

A.180°
B.360°
C.1 620°
D.1 980°

答案： B
∵任意多边形的外角和都等于 360°，
∴正十一边形的外角和为 360°. 故选 B.

4.跨化学·分子结构(2024广西桂林二模)C₆₀是单纯由碳原子结合形成的稳定分子,它的发现最初于天文学领域的研究,由英国、美国科学家探明和勾画其碳分子结构,于1985年正式制得,它的发现使人类了解到一个全新的碳世界.如图所示的是C₆₀的分子结构图,它具有60个顶点和32个面,其中12个面为正五边形,20个面为正六边形,则正六边形的每一个内角的度数是 ( )

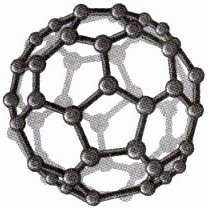
A.60°
B.72°
C.108°
D.120°

答案： D 正六边形的内角和为(6 - 2)×180° = 720°，
∵正六边形的 6 个内角都相等，
∴正六边形的每一个内角的度数是 720°÷6 = 120°. 故选 D.

5.(2024湖南长沙望城月考)已知正x边形的内角和为1 080°,边长为2.
(1)求正x边形的周长.
(2)若正n边形的每个外角的度数比正x边形每个内角的度数小63°,求n的值.

答案： **解析**
(1)由题意可得(x - 2)×180° = 1080°，解得 x = 8，
∴正 x 边形的周长为 8×2 = 16.
(2)由
(1)知正八边形每个内角的度数为 1080°÷8 = 135°，
∴正 n 边形的每个外角的度数为 135° - 63° = 72°，
∵360°÷72° = 5，
∴n 的值为 5.

6.下列图形中,具有稳定性的是 ( )

答案： A 三角形具有稳定性，四边形具有不稳定性. 故选 A.

7.(2024内蒙古赤峰中考,7,★★☆)下图是正n边形纸片的一部分,其中l,m是正n边形两条边的一部分,若l,m所在的直线相交而形成的锐角为60°,则n的值是(M8202001) ( )

A.5
B.6
C.8
D.10

答案： B 如图，l，m 所在的直线相交于点 A，则∠A = 60°，
∴正 n 边形的每个外角为∠1 = ∠2 = $\frac{180° - 60°}{2}$ = 60°，
∴n = 360°÷60° = 6. 故选 B.

8.(2023湖南怀化新晃期中,4,★★☆)如图,若干个全等正五边形排成环状.图中所示的是前3个正五边形,要完成这一圆环还需正五边形的个数为 ( )

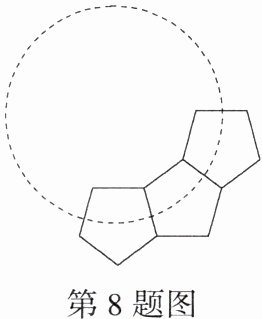
A.6
B.7
C.8
D.9

答案： B 正五边形的一个内角为(5 - 2)×180°÷5 = 108°，如图，延长正五边形的两边相交于点 O，则∠1 = 360° - 108°×3 = 36°，360°÷36° = 10，
∵已经有 3 个正五边形，10 - 3 = 7，
∴完成这一圆环还需 7 个正五边形. 故选 B.

9.(2023四川遂宁期末,7,★★☆)能够铺满地面的正多边形组合是 ( )
A.正六边形和正方形
B.正五边形和正八边形
C.正方形和正八边形
D.正三角形和正八边形

答案： C 设正多边形的个数分别是 m，n(m，n 为正整数).
A. 正六边形的每个内角是 120°，正方形的每个内角是 90°，120°m + 90°n = 360°，显然 m，n 不能同时取正整数，故不能铺满；B. 正五边形每个内角是 108°，正八边形每个内角为 135°，135°m + 108°n = 360°，显然 m，n 不能同时取正整数，故不能铺满；C. 正方形的每个内角为 90°，正八边形的每个内角为 135°，两个正八边形和一个正方形刚好能拼出一个 360°的角，故能铺满；D. 正三角形每个内角为 60°，正八边形每个内角为 135°，60°m + 135°n = 360°，显然 m，n 不能同时取正整数，故不能铺满. 故选 C.
**方法归纳**
正多边形镶嵌问题的解题关键：围绕一点拼在一起的正多边形的内角加在一起恰好组成一个周角. 分别求出各个正多边形的每个内角的度数，结合镶嵌的条件即可求出答案.