《2025年5年中考3年模拟八年级数学下册湘教版》

1.如图所示的图形中,多边形的个数为 （ ）

A.3
B.4
C.5
D.6

答案： A 在平面内，由一些线段首尾顺次相接组成的封闭图形叫作多边形. 题图中，多边形有三角形、四边形和六边形，共 3 个.

2.教材变式·P36练习T2 从六边形的一个顶点出发,可以画出x条对角线,它们将六边形分成y个三角形,则x,y的值分别为 （ ）
A.4,3
B.3,3
C.3,4
D.4,4

答案： C 因为从 $n$ 边形的一个顶点出发，可以画的对角线的条数是 $n - 3$，分成的三角形个数是 $n - 2$，所以 $x=6 - 3 = 3$，$y = 6 - 2 = 4$. 故选 C.

3.(2024广西百色田阳一模)若一个多边形的内角和等于900°,则这个多边形的边数是 （ ）
A.8
B.7
C.6
D.5

答案： B 设多边形的边数为 $n$，则 $(n - 2)\cdot180^{\circ}=900^{\circ}$，解得 $n = 7$. 故选 B.

4.如图,已知六边形ABCDEF的每个内角都相等,连接AD.
(1)若∠1 = 48°,求∠2的度数.
(2)求证:AB//DE.

答案： 解析 \n（1）$\because$ 六边形 $ABCDEF$ 的每个内角都相等，$\therefore$ 每个内角的大小为 $\frac{(6 - 2)\times180^{\circ}}{6}=120^{\circ}$，$\therefore\angle E=\angle F=\angle BAF = 120^{\circ}$. $\because\angle1 = 48^{\circ}$，$\therefore\angle FAD=\angle FAB-\angle1 = 120^{\circ}-48^{\circ}=72^{\circ}$，$\because\angle2+\angle FAD+\angle F+\angle E = 360^{\circ}$，$\therefore\angle2 = 360^{\circ}-\angle FAD-\angle F-\angle E = 360^{\circ}-72^{\circ}-120^{\circ}-120^{\circ}=48^{\circ}$.\n（2）证明：由（1）知 $\angle BAF=\angle E=\angle F = 120^{\circ}$，$\therefore\angle1 = 120^{\circ}-\angle DAF$，$\angle2 = 360^{\circ}-120^{\circ}-120^{\circ}-\angle DAF = 120^{\circ}-\angle DAF$，$\therefore\angle1=\angle2$，$\therefore AB// DE$.

5.(2024湖南怀化新晃期中,8,★☆☆)在学习完多边形后,小华同学将一个五边形沿直线l剪掉一个角后,得到一个新多边形如图所示,下列说法正确的是 （ ）

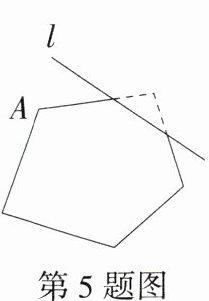
A.这个新多边形是一个五边形
B.从这个新多边形的顶点A出发,最多可以画4条对角线
C.从顶点A出发的所有对角线将这个新多边形分成4个三角形
D.以上说法都不正确

答案： C 由题图可得减掉一个角后所得的新多边形为六边形，故 A 选项错误；从六边形的顶点 $A$ 出发，最多可以画 $6 - 3 = 3$（条）对角线，故 B 选项错误；从顶点 $A$ 出发的所有对角线将六边形分成的三角形个数为 $6 - 2 = 4$，故 C 选项正确，D 选项错误. 故选 C.

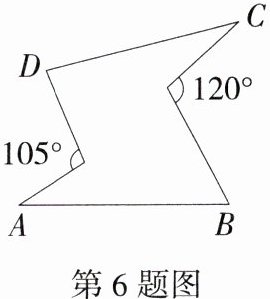
6.(2024湖南娄底新化期末,16,★★☆)如图,∠A + ∠B + ∠C + ∠D = ________.

答案：
答案 $225^{\circ}$\n解析：如图，连接 $AD$，$BC$，\n$\because\angle DEA+\angle EAD+\angle ADE = 180^{\circ}$，$\angle DEA = 105^{\circ}$，$\therefore\angle EAD+\angle ADE = 180^{\circ}-105^{\circ}=75^{\circ}$，\n$\because\angle CFB+\angle FCB+\angle FBC = 180^{\circ}$，$\angle CFB = 120^{\circ}$，$\therefore\angle FCB+\angle FBC = 180^{\circ}-120^{\circ}=60^{\circ}$，\n$\because$ 在四边形 $ABCD$ 中，$\angle DAB+\angle ABC+\angle BCD+\angle CDA = 360^{\circ}$，\n$\therefore\angle DCF+\angle ABF+\angle EAB+\angle EDC = 360^{\circ}-(\angle EAD+\angle ADE)-(\angle FCB+\angle FBC)=360^{\circ}-75^{\circ}-60^{\circ}=225^{\circ}$.

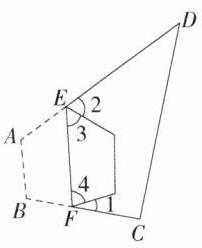
7.(2023河南郑州枫杨外国语学校期末,16,★★☆)如图,E,F分别是四边形ABCD的边AD,BC上的点,连接EF,将四边形ABCD沿直线EF折叠.若点A,B都落在四边形ABCD的内部,记∠C + ∠D = α,则∠1 + ∠2 = ________.(用含α的式子表示)

答案：
答案 $360^{\circ}-2\alpha$\n解析：如图，$\because\angle A+\angle B+\angle C+\angle D = 360^{\circ}$，$\angle C+\angle D=\alpha$，$\therefore\angle A+\angle B = 360^{\circ}-\alpha$，\n$\because\angle A+\angle B+\angle AEF+\angle BFE = 360^{\circ}$，$\therefore\angle AEF+\angle BFE = 360^{\circ}-(\angle A+\angle B)=\alpha$，\n由折叠可得 $\angle3+\angle4=\angle AEF+\angle BFE=\alpha$，$\therefore\angle1+\angle2 = 360^{\circ}-2\alpha$，故答案为 $360^{\circ}-2\alpha$.

8.(2024湖南岳阳期中改编,21,★★☆)阅读小明和小红的对话,解决下列问题.

(1)这个“多加的锐角”的度数是 ________°.
(2)小明求的是 ________边形的内角和.

答案： 答案 （1）$30$ （2）十二\n解析 \n（1）多边形的内角和是 $180^{\circ}$ 的整数倍，$1800^{\circ}=180^{\circ}\times10$，$1830^{\circ}-1800^{\circ}=30^{\circ}$，故答案为 $30$.\n（2）设小明求的多边形的边数为 $x$，依题意有 $(x - 2)\cdot180^{\circ}＜1830^{\circ}$，解得 $x＜12\frac{1}{6}$. $\because x$ 为大于或等于 $3$ 的整数，且多加了一个锐角，$\therefore$ 多边形的边数是 $12$，故小明求的是十二边形的内角和.